函数 $f\left( x \right) = 3\sin \left( {2x + \dfrac{{\mathrm \pi} }{6}} \right)$ 的部分图象如图所示.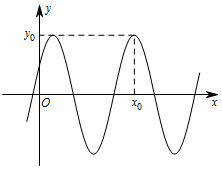

【难度】
【出处】
2014年高考北京卷(文)
【标注】
-
写出 $f\left( x \right)$ 的最小正周期及图中 ${x_0}$,${y_0}$ 的值;标注答案$f\left( x \right)$ 的最小正周期为 ${\mathrm \pi} $,${x_0} = \dfrac{{7{\mathrm \pi} }}{6}$,${y_0} = 3$解析本题考查正弦型函数的图象与性质.由 $f\left( x \right) = 3\sin \left( {2x + \dfrac{{\mathrm \pi} }{6}} \right)$ 可知,$f\left( x \right)$ 的最小正周期 $T=\dfrac{2{\mathrm \pi} }{2}={\mathrm \pi} $,${x_0} =\dfrac{\mathrm \pi} {6}+{\mathrm \pi} = \dfrac{{7{\mathrm \pi} }}{6}$,${y_0} = 3$.
-
求 $f\left( x \right)$ 在区间 $\left[ { - \dfrac{{\mathrm \pi} }{2}, - \dfrac{{\mathrm \pi} }{12}} \right]$ 上的最大值和最小值.标注答案最大值 $ 0 $;最小值 $ - 3$解析根据 $x$ 的范围可以确定 $\omega x+\varphi$ 的范围,进而判断此函数的最值.因为 $x \in \left[ - \dfrac{{\mathrm \pi} }{2}, - \dfrac{{\mathrm \pi} }{12}\right]$,所以\[2x + \dfrac{{\mathrm \pi} }{6} \in \left[ - \dfrac{{5{\mathrm \pi} }}{6},0\right],\]于是,当 $2x + \dfrac{{\mathrm \pi} }{6} = 0$,即 $x = - \dfrac{{\mathrm \pi} }{12}$ 时,$f\left( x \right)$ 取得最大值 $ 0 $;
当 $2x + \dfrac{{\mathrm \pi} }{6} = - \dfrac{{\mathrm \pi} }{2}$,即 $x = - \dfrac{{\mathrm \pi} }{3}$ 时,$f\left( x \right)$ 取得最小值 $ - 3$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2