从某校随机抽取 $ 100 $ 名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:\[ \begin{array}{|c|c|c|} \hline
组号 & 分组 & 频数 \\ \hline
1 & \left[0,2\right)& 6 \\ \hline
2 & \left[2,4\right)& 8 \\ \hline
3 & \left[4,6\right)& 17 \\ \hline
4 & \left[6,8\right)& 22 \\ \hline
5 & \left[8,10\right)& 25 \\ \hline
6 & \left[10,12\right)& 12 \\ \hline
7 & \left[12,14\right)& 6 \\ \hline
8 & \left[14,16\right)& 2 \\ \hline
9 & \left[16,18\right)& 2 \\ \hline
合计 & & 100 \\ \hline \end{array} \]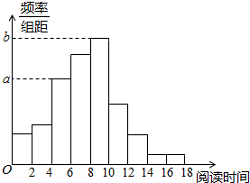
组号 & 分组 & 频数 \\ \hline
1 & \left[0,2\right)& 6 \\ \hline
2 & \left[2,4\right)& 8 \\ \hline
3 & \left[4,6\right)& 17 \\ \hline
4 & \left[6,8\right)& 22 \\ \hline
5 & \left[8,10\right)& 25 \\ \hline
6 & \left[10,12\right)& 12 \\ \hline
7 & \left[12,14\right)& 6 \\ \hline
8 & \left[14,16\right)& 2 \\ \hline
9 & \left[16,18\right)& 2 \\ \hline
合计 & & 100 \\ \hline \end{array} \]

【难度】
【出处】
2014年高考北京卷(文)
【标注】
-
从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于 $ 12 $ 小时的概率;标注答案$0.9$解析本题考查频率分布表的相关问题.根据频数分布表,$ 100 $ 名学生中课外阅读时间不少于 $ 12 $ 小时的学生共有 $ 6+2+2=10 $ 名,所以样本中的学生课外阅读时间少于 $ 12 $ 小时的频率是\[1 - \dfrac{10}{100} = 0.9.\]从该校随机选取一名学生,估计这名学生该周课外阅读时间少于 $ 12 $ 小时的概率为 $0.9$.
-
求频率分布直方图中的 $ a,b $ 的值;标注答案$ a = 0.085 $;$ b =0.125 $解析本题考查频率分布直方图的相关问题.课外阅读时间落在组 $\left[4,6\right)$ 的有 $ 17 $ 人,频率为 $0.17$,所以\[a \overset{\left[a\right]}= \dfrac{频率}{组距} = \dfrac{0.17}{2} = 0.085,\]课外阅读时间落在组 $\left[8,10\right)$ 的有 $ 25 $ 人,频率为 $0.25$,所以\[b \overset{\left[a\right]}= \dfrac{频率}{组距} = \dfrac{0.25}{2} = 0.125.\](推导中用到:$\left[a\right]$)
-
假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的 $ 100 $ 名学生该周课外阅读时间的平均数在第几组.(只需写出结论)标注答案第 $ 4 $ 组解析本题考查样本数据的数字特征相关问题.依题意,估计样本中的 $ 100 $ 名学生课外阅读时间的平均数为\[\begin{split}\overline x&=\dfrac{6\times 1+8\times 3+17\times 5+\cdots +6\times 13+2\times 15+2\times 17}{100}\\&=7.68,\end{split} \]故在第 $ 4 $ 组.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3