如图，已知 $AA_1\perp 平面ABC$，$BB_1 \parallel AA_1$，$AB=AC=3$，$BC=2\sqrt 5$，$AA_1=\sqrt 7$，$BB_1=2\sqrt 7$，点 $E$ 和 $F$ 分别为 $BC$ 和 $A_1C $ 的中点．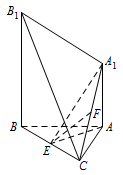
【难度】
【出处】
2015年高考天津卷（文）
【标注】
-
求证：$EF \parallel 平面A_1B_1BA$；标注答案略解析本小题是证明线面平行，关键是在平面内找一条与已知直线平行的直线．如图，连接 $A_1B$．
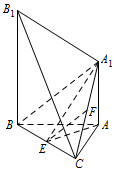在 $\triangle A_1BC$ 中，因为 $E$ 和 $F$ 分别是 $BC$ 和 $A_1C$ 的中点，
所以 $EF \parallel BA_1$．
又因为 $EF\not\subset 平面A_1B_1BA$，$ BA_1\subset 平面A_1B_1BA$，
所以 $EF \parallel 平面A_1B_1BA$． -
求证：$平面 AEA_1\perp 平面BCB_1$；标注答案略解析本小题是证明面面垂直，在一个平面内找另外一个平面的一条垂线即可．因为 $AB=AC$，$E$ 为 $BC$ 的中点，
所以 $AE\perp BC$．
因为 $AA_1\perp 平面ABC$，$BB_1 \parallel A_1A$，
所以 $BB_1\perp 平面ABC$，从而 $BB_1\perp AE$．
又因为 $BC\cap BB_1=B$，
所以 $AE\perp 平面BCB_1$．
又因为 $AE\subset 平面AEA_1$，
所以 $平面AEA_1\perp 平面BCB_1$． -
求直线 $A_1B_1$ 与平面 $BCB_1$ 所成角的大小．标注答案$30^\circ$解析几何法求线面角的关键是作出（或找到）线面角，然后再解直角三角形．如图，取 $BB_1$ 的中点 $M$ 和 $B_1C$ 的中点 $N$，连接 $A_1M$，$A_1N$，$NE$．
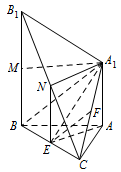因为 $N$ 和 $E$ 分别为 $B_1C$ 和 $BC$ 的中点，
所以 $NE \parallel B_1B$，$NE=\dfrac 12B_1B$，故 $NE \parallel A_1A$，且 $NE=A_1A$，
所以四边形 $A_1NEA$ 为平行四边形，$A_1N \parallel AE$，且 $A_1N=AE$．
又因为 $AE\perp 平面BCB_1$，
所以 $A_1N\perp 平面BCB_1$，从而 $\angle A_1B_1N$ 为直线 $A_1B_1$ 与平面 $BCB_1$ 所成的角．
在 $\triangle ABC$ 中，可得 $AE=2$，
所以 $A_1N=AE=2$．
因为 $BM \parallel AA_1$，$BM=AA_1$，
所以 $A_1M \parallel AB$，$A_1M=AB$．
又 $AB\perp BB_1$，所以 $A_1M\perp BB_1$．
在 $\mathrm {Rt}\triangle {A_1MB_1}$ 中，可得 $A_1B_1=\sqrt {B_1M^2+A_1M^2}=4$．
在 $\mathrm {Rt}\triangle {A_1NB_1}$ 中，可得 $\sin \angle {A_!B_1N}=\dfrac {A_1N}{A_1B_1}=\dfrac 12$．
因此 $\angle A_1B_1N=30^\circ $．
所以，直线 $A_1B_1$ 与平面 $BCB_1$ 所成的角为 $30^\circ$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
