$2$

本小题属于椭圆的基本量问题．设 $F\left(-c,0\right)$．
由已知得 $\dfrac ca=\dfrac {\sqrt 5}{5}$，又 $a^2=b^2+c^2$，可得 $a=\sqrt 5c$，$b=2c$，
又因为 $B\left(0,b\right)$，$F\left(-c,0\right)$，
所以直线 $BF$ 的斜率 $k=\dfrac {b-0}{0-\left(-c\right)}=\dfrac {2c}{c}=2$．

① $\dfrac 78$
② $\dfrac {x^2}{5}+\dfrac {y^2}{4}=1$

可以先计算 $P$，$Q$ 两点的横坐标，然后计算 $\lambda$；在第 ① 小问的提示下将第 ② 小问的条件稍加转化就可以顺利求解．如果在计算 $P$，$Q$ 两点的坐标时注意到两者的相关性，那么就可以通过一次联立两次赋值求出坐标，从而简化运算．如图，设点 $P\left(x_p,y_p\right)$，$Q\left(x_Q,y_Q\right)$，$M\left(x_M,y_M\right)$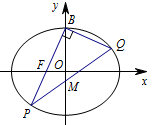．① 由（1）可得椭圆方程为 $\dfrac {x^2}{5c^2}+\dfrac {y^2}{4c^2}=1$，直线 $BF$ 方程为 $y=2x+2c$，将直线方程与椭圆方程联立，消去 $y$，整理得\[3x^2+5cx=0 ,\]解得 $x_p=-\dfrac {5c}{3}$．
因为 $BQ\perp BP$，
所以直线 $BQ$ 的方程为 $y=-\dfrac 12x+2c$，与椭圆方程联立，消去 $y$，整理得\[21x^2-40cx=0 ,\]解得 $x_Q=\dfrac {40c}{21}$．
又因为 $ \left|PM \right|=\lambda \left|MQ \right|$，$x_M=0$，所以 $\overrightarrow{PM}=\lambda\overrightarrow{MQ}$，$x_M-x_P=\lambda\left(x_Q-x_M\right)$，所以\[\lambda=\dfrac { \left|x_P \right|}{ \left|x_Q \right|}=\dfrac 78.\]② 由 ① 有 $\dfrac { \left|PM \right|}{ \left|MQ \right|}=\dfrac 78$，
所以 $\dfrac { \left|PM \right|}{ \left|PM \right|+ \left|MQ \right|}=\dfrac {7}{7+8}=\dfrac {7}{15}$，即 $ \left|PQ \right|=\dfrac {15}{7} \left|PM \right|$．
又因为 $ \left|PM \right|\sin \angle BQP=\dfrac {7\sqrt 5}{9}$，所以\[\begin{split}\left|BP \right|&= \left|PQ \right|\sin \angle BQP\\&=\dfrac {15}{7} \left|PM \right|\sin \angle BQP\\&=\dfrac {5\sqrt 5}{3}.\end{split}\]又因为 $y_P=2x_P+2c=-\dfrac 43c$，所以\[\begin{split}\left|BP \right|&=\sqrt {\left(0+\dfrac {5c}{3}\right)^2+\left(2c+\dfrac {4c}{3}\right)^2}\\&=\dfrac {5\sqrt 5}{3}c.\end{split}\]因此 $\dfrac {5\sqrt 5}{3}c=\dfrac {5\sqrt 5}{3}$，得 $c=1$．
所以，椭圆的方程为 $\dfrac {x^2}{5}+\dfrac {y^2}{4}=1$．