如图，长方体 $ABCD-A_1B_1C_1D_1$ 中 $AB=16$，$BC=10$，$AA_1=8$，点 $E$，$F$ 分别在 $A_1B_1$，$D_1C_1$ 上，$A_1E=D_1F=4$．过点 $E$，$F$ 的平面 $\alpha$ 与此长方体的面相交，交线围成一个正方形．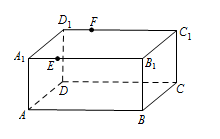
【难度】
【出处】
2015年高考全国II卷（文）
【标注】
-
在图中画出这个正方形（不必说明画法与理由）；标注答案略解析本小题其实就是要求作出符合条件的长方体的截面．交线围成的正方形 $EHGF$ 如图．
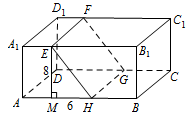注：具体画法为，在 $AB$ 上取 $AH=10$，在 $DC$ 上取 $DG=10$，连接 $EH$，$HG$，$GF$ 即可． -
求平面 $\alpha$ 把该长方体分成的两部分体积的比值．标注答案$\dfrac{9}{7}$（$\dfrac{7}{9}$ 也正确）解析本小题是空间几何体的体积比较问题，因为两个四棱柱等高，所以只要求它们底面面积的比即可．作 $EM\perp AB$，垂足为 $M$，则 $AM=A_1E=4$，$EB_1=12$，$EM=AA_1=8$．
因为 $EHGF$ 为正方形，所以 $EH=EF=BC=10$．
于是 $MH=\sqrt{EH^2-EM^2}=6$，
$AH=10$，$HB=6$．
故 $S_{四边形A_1EHA}=\dfrac 12\times \left(4+10\right)\times 8=56$，$S_{四边形EB_1BH}=\dfrac 12\times \left(12+6\right)\times 8=72$．
因为长方体被平面 $\alpha$ 分为两个高为 $10$ 的直棱柱，所以其体积的比值为 $\dfrac{9}{7}$（$\dfrac{7}{9}$ 也正确）．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
