如图，$O$ 为等腰三角形 $ABC$ 内一点，$\odot O$ 与 $\triangle ABC$ 的底边 $BC$ 交于 $M$，$N$ 两点，与底边上的高 $AD$ 交于点 $G$，且与 $AB$，$AC$ 分别相切于 $E$，$F$ 两点．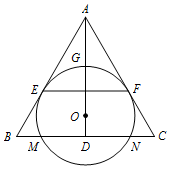
【难度】
【出处】
2015年高考全国II卷（理）
【标注】
-
证明：$EF\parallel BC$；标注答案略解析本小题主要考查切线长定理．$\because \triangle ABC$ 为等腰三角形且 $BC$ 为底边，
$\therefore AB=AC$．
又 $AB$、$AC$ 切 $\odot O$ 于 $E$、$F$，
$\therefore AE=AF$，
$\therefore$ 在 $\triangle AEF$ 与 $\triangle ABC$ 中，$\angle AEF=\dfrac 12\left({\mathrm \pi} -\angle EAF\right)=\angle ABC$，
$\therefore EF\parallel BC$． -
若 $AG$ 等于 $\odot O$ 的半径，且 $AE=MN=2\sqrt 3$，求四边形 $EBCF$ 的面积．标注答案$\dfrac{16\sqrt 3}{3}$解析本小题综合考查圆的切线的性质、等边三角形的判定、相似三角形的性质等知识点．连接 $OE$，$OM$，则 $OE\perp AB$．
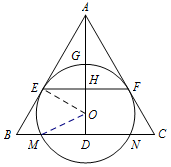设圆的半径为 $r$，则在 ${\mathrm {Rt}}\triangle AEO$ 中，
$AO^2=AE^2+OE^2$，即 $\left(2r\right)^2=\left(2\sqrt 3\right)^2+r^2$，
故 $r=2$，
$\therefore \angle EAO=\dfrac{\mathrm \pi} {6}$，$\angle EOG=\dfrac{\mathrm \pi} {3}$，
$\therefore \angle ABC=\dfrac{\mathrm \pi} {3}$，$EF=2\sqrt 3$．
$\therefore \triangle AEF$ 与 $\triangle ABC$ 为等边三角形，
在 ${\mathrm {Rt}}\triangle DMO$ 中，$MD=\sqrt 3$，$OM=2$，所以 $OD=1$．
$\therefore S_{\triangle AEF}=\dfrac{\sqrt 3}{4}AE^2=3\sqrt 3$，
$\because \dfrac{S_{\triangle AEF}}{S_{\triangle ABC}}=\left(\dfrac{AH}{AD}\right)^2=\dfrac{9}{25}$，
$\therefore S_{ 四边形 EFCB}=\dfrac {16}{9}\times S_{\triangle AEF}=\dfrac{16\sqrt 3}{3}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
