$ 20 $ 名学生某次数学考试成绩(单位:分)的频率分布直方图如下: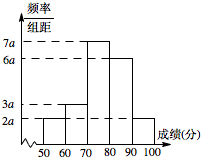

【难度】
【出处】
2014年高考重庆卷(文)
【标注】
-
求频率分布直方图中 $ a$ 的值;标注答案$ \dfrac{1}{200} = 0.005$.解析本题可利用所有小矩形的面积之和为 $1$ 求解.据直方图知,组距为 $ 10 $,由 $\left( {2a + 3a + 6a + 7a + 2a} \right) \times 10 = 1$解得\[a = \dfrac{1}{200} = 0.005.\]
-
分别求出成绩落在 $ \left[50,60\right)$ 与 $ \left[60,70\right)$ 中的学生人数;标注答案$2$,$3$.解析总人数乘以相应频率即可.根据频率分布直方图得,成绩落在 $\left[ {50,60} \right)$ 中的学生人数为\[2 \times 0.005 \times 10 \times 20 = 2,\]成绩落在 $\left[ {60,70} \right)$ 中的学生人数为\[3 \times 0.005 \times 10 \times 20 = 3.\]
-
从成绩在 $ \left[50,70\right)$ 的学生中任选 $ 2 $ 人,求此 $ 2 $ 人的成绩都在 $ \left[60,70\right)$ 中的概率标注答案$ \dfrac{3}{10}$.解析本题即求从 $5$ 人中任选 $2$ 人,$2$ 人都在 $[60,70)$ 中的概率.记成绩落在 $\left[ {50 , 60} \right)$ 中的 $ 2 $ 人为 ${A_1},{A_2}$,
成绩落在 $\left[ {60,70} \right)$ 中的 $ 3 $ 人为 ${B_1},{B_2},{B_3}$,
则从成绩在 $\left[ {50 , 70} \right)$ 的学生中任选 $ 2 $ 人的基本事件共有 $ 10 $ 个:
$ \left( {{A_1},{A_2}} \right) $,$ \left( {{A_1},{B_1}} \right) $,$ \left( {{A_1},{B_2}} \right) $,$ \left( {{A_1},{B_3}} \right) $,$ \left( {{A_2},{B_1}} \right) $,
$ \left( {{A_2},{B_2}} \right) $,$ \left( {{A_2},{B_3}} \right) $,$ \left( {{B_1},{B_2}} \right) $,$ \left( {{B_1},{B_3}} \right) $,$ \left( {{B_2},{B_3}} \right) $,
其中 $ 2 $ 人的成绩都在 $ \left[60,70\right)$ 中的基本事件有 $ 3 $ 个:\[\left( {{B_1},{B_2}} \right),\left( {{B_1},{B_3}} \right),\left( {{B_2},{B_3}} \right),\]故依古典概型概率计算公式得所求概率为 $P = \dfrac{3}{10}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3