如图,四棱锥 $P-ABCD $ 中,底面是以 $O $ 为中心的菱形,$PO\perp $ 底面 $ ABCD$,$ AB=2$,$\angle BAD=\dfrac {\mathrm \pi} 3$,$ M$ 为 $BC $ 上一点,且 $BM=\dfrac 12 $.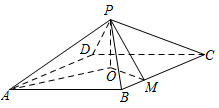

【难度】
【出处】
2014年高考重庆卷(文)
【标注】
-
证明:$BC\perp $ 平面 $POM $;标注答案略.解析本题的关键在求证 $BM\perp OM$,可用余弦定理证得.如图,$ABCD$ 为菱形,$O$ 为菱形中心,连接 $OB$,则 $AO \perp OB$,
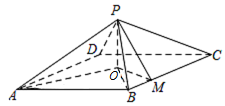 因为 $\angle BAD = \dfrac{{\mathrm \pi} }{3}$,故\[OB = AB \cdot \sin \angle OAB = 2\sin \dfrac{\mathrm \pi} {6} = 1.\]又因为 $BM = \dfrac{1}{2}$,且 $\angle OBM = \dfrac{\mathrm \pi} {3}$,在 $\triangle OBM$ 中根据余弦定理可得\[\begin{split}O{M^2} &= O{B^2} + B{M^2} - 2OB \cdot BM \cdot \cos \angle OBM \\&= {1^2} + {\left( {\dfrac{1}{2}} \right)^2} - 2 \times 1 \times \dfrac{1}{2} \times \cos \dfrac{\mathrm \pi} {3} = \dfrac{3}{4},\end{split}\]所以\[O{B^2} = O{M^2} + B{M^2},\]故 $OM \perp BM$.
因为 $\angle BAD = \dfrac{{\mathrm \pi} }{3}$,故\[OB = AB \cdot \sin \angle OAB = 2\sin \dfrac{\mathrm \pi} {6} = 1.\]又因为 $BM = \dfrac{1}{2}$,且 $\angle OBM = \dfrac{\mathrm \pi} {3}$,在 $\triangle OBM$ 中根据余弦定理可得\[\begin{split}O{M^2} &= O{B^2} + B{M^2} - 2OB \cdot BM \cdot \cos \angle OBM \\&= {1^2} + {\left( {\dfrac{1}{2}} \right)^2} - 2 \times 1 \times \dfrac{1}{2} \times \cos \dfrac{\mathrm \pi} {3} = \dfrac{3}{4},\end{split}\]所以\[O{B^2} = O{M^2} + B{M^2},\]故 $OM \perp BM$.
又 $PO \perp $ 底面 $ABCD$,所以 $PO \perp BC$,从而 $BC$ 与平面 $POM$ 内两条相交直线 $OM$,$PO$ 都垂直,
所以 $BC \perp $ 平面 $POM$. -
若 $MP\perp AP $,求四棱锥 $P-ABMO $ 的体积.标注答案$\dfrac{5}{16}$.解析本题的关键在于求棱锥的高,即 $PO$ 长.可根据 $\triangle PAM$ 为直角三角形,利用勾股定理建立方程求得.由(1)可知,\[OA = AB \cdot \cos \angle OAB = 2 \cdot \cos \dfrac{{\mathrm \pi} }{6} = \sqrt 3 ,\]
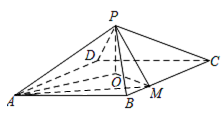 设 $PO = a$,由 $PO \perp $ 底面 $ABCD$ 知,$\triangle POA$ 为直角三角形,故\[P{A^2} = P{O^2} + O{A^2} = {a^2} + 3,\]由 $\triangle POM$ 也是直角三角形,故\[P{M^2} = P{O^2} + O{M^2} = {a^2} + \dfrac{3}{4},\]连接 $AM$,在 $\triangle ABM$ 中,根据余弦定理得\[\begin{split}A{M^2} &= A{B^2} + B{M^2} - 2AB \cdot BM \cdot \cos \angle ABM \\&= {2^2} + {\left( {\dfrac{1}{2}} \right)^2} - 2 \cdot 2 \cdot \dfrac{1}{2} \cdot \cos \dfrac{{2{\mathrm \pi} }}{3} \\&= \dfrac{21}{4},\end{split}\]由已知 $MP \perp AP$,故 $\triangle APM$ 为直角三角形,则 $P{A^2} + P{M^2} = A{M^2}$,即\[{a^2} + 3 + {a^2} + \dfrac{3}{4} = \dfrac{21}{4},\]得\[a = \dfrac{\sqrt 3 }{2},a = - \dfrac{\sqrt 3 }{2} \left(舍去\right),\]即 $PO = \dfrac{\sqrt 3 }{2}$,此时\[\begin{split}{S_{ABMO}} &= {S_{\triangle AOB}} + {S_{\triangle OMB}} \\&= \dfrac{1}{2} \cdot AO \cdot OB + \dfrac{1}{2} \cdot BM \cdot OM\\&= \dfrac{1}{2} \cdot \sqrt 3 \cdot 1 + \dfrac{1}{2} \cdot \dfrac{1}{2} \cdot \dfrac{\sqrt 3 }{2} \\&= \dfrac{5\sqrt 3 }{8},\end{split}\]所以四棱锥 $P - ABMO$ 的体积为\[\begin{split}{V_{P - ABMO}} &= \dfrac{1}{3} \cdot {S_{ABMO}} \cdot PO \\&= \dfrac{1}{3} \cdot \dfrac{5\sqrt 3 }{8} \cdot \dfrac{\sqrt 3 }{2} \\&= \dfrac{5}{16}.\end{split}\]
设 $PO = a$,由 $PO \perp $ 底面 $ABCD$ 知,$\triangle POA$ 为直角三角形,故\[P{A^2} = P{O^2} + O{A^2} = {a^2} + 3,\]由 $\triangle POM$ 也是直角三角形,故\[P{M^2} = P{O^2} + O{M^2} = {a^2} + \dfrac{3}{4},\]连接 $AM$,在 $\triangle ABM$ 中,根据余弦定理得\[\begin{split}A{M^2} &= A{B^2} + B{M^2} - 2AB \cdot BM \cdot \cos \angle ABM \\&= {2^2} + {\left( {\dfrac{1}{2}} \right)^2} - 2 \cdot 2 \cdot \dfrac{1}{2} \cdot \cos \dfrac{{2{\mathrm \pi} }}{3} \\&= \dfrac{21}{4},\end{split}\]由已知 $MP \perp AP$,故 $\triangle APM$ 为直角三角形,则 $P{A^2} + P{M^2} = A{M^2}$,即\[{a^2} + 3 + {a^2} + \dfrac{3}{4} = \dfrac{21}{4},\]得\[a = \dfrac{\sqrt 3 }{2},a = - \dfrac{\sqrt 3 }{2} \left(舍去\right),\]即 $PO = \dfrac{\sqrt 3 }{2}$,此时\[\begin{split}{S_{ABMO}} &= {S_{\triangle AOB}} + {S_{\triangle OMB}} \\&= \dfrac{1}{2} \cdot AO \cdot OB + \dfrac{1}{2} \cdot BM \cdot OM\\&= \dfrac{1}{2} \cdot \sqrt 3 \cdot 1 + \dfrac{1}{2} \cdot \dfrac{1}{2} \cdot \dfrac{\sqrt 3 }{2} \\&= \dfrac{5\sqrt 3 }{8},\end{split}\]所以四棱锥 $P - ABMO$ 的体积为\[\begin{split}{V_{P - ABMO}} &= \dfrac{1}{3} \cdot {S_{ABMO}} \cdot PO \\&= \dfrac{1}{3} \cdot \dfrac{5\sqrt 3 }{8} \cdot \dfrac{\sqrt 3 }{2} \\&= \dfrac{5}{16}.\end{split}\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2