查看数据源：599165c52bfec200011e0c26
设椭圆 $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1 \left(a > b > 0\right) $ 的左、右焦点分别为 ${F_1}、{F_2}$，点 $D$ 在椭圆上，$D{F_1} \perp {F_1}{F_2}$，$\dfrac{{|{F_1}{F_2}|}}{{|D{F_1}|}} = 2\sqrt 2 $，$\triangle D{F_1}{F_2}$ 的面积为 $\dfrac{\sqrt 2 }{2}$．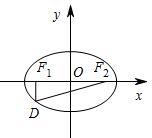
【难度】
【出处】
无
【标注】
  1. 求该椭圆的标准方程；
    标注
    答案
    $\dfrac{x^2}{2} + {y^2} = 1$．
    解析
    本题给出焦点三角形 $DF_1F_2$，这提示我们应用椭圆定义，又焦点三角形为直角三角形，于是我们可以对焦点三角形应用勾股定理，结合题中条件，可求出 $a,b$．设 ${F_1}\left( { - c,0} \right)$，${F_2}\left( {c,0} \right)$，其中 ${c^2} = {a^2} - {b^2} $，由 $\dfrac{{\left| {{F_1}{F_2}} \right|}}{{\left| {D{F_1}} \right|}} = 2\sqrt 2 $，得\[\left| {D{F_1}} \right| = \dfrac{{\left| {{F_1}{F_2}} \right|}}{2\sqrt 2 } = \dfrac{\sqrt 2 }{2}c,\]从而\[{S_{\triangle D{F_1}{F_2}}} = \dfrac{1}{2}\left| {D{F_1}} \right| \cdot \left| {{F_1}{F_2}} \right| = \dfrac{\sqrt 2 }{2}{c^2} = \dfrac{\sqrt 2 }{2},\]解得 $c = 1$．从而 $\left| {D{F_1}} \right| = \dfrac{\sqrt 2 }{2}$，由 $D{F_1} \perp {F_1}{F_2}$，得\[{\left| {D{F_2}} \right|^2} = {\left| {D{F_1}} \right|^2} + {\left| {{F_1}{F_2}} \right|^2} = \dfrac{9}{2},\]因此 $\left| {D{F_2}} \right| = \dfrac{3\sqrt 2 }{2}$，根据椭圆的定义有\[2a = \left| {D{F_1}} \right| + \left| {D{F_2}} \right| = 2\sqrt 2 ,\]即 $a = \sqrt 2$，所以 ${b^2} = {a^2} - {c^2} = 1$，因此，所求椭圆的标准方程为 $\dfrac{x^2}{2} + {y^2} = 1$．
  2. 设圆心在 $y$ 轴上的圆与椭圆在 $x$ 轴的上方有两个交点，且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点，求圆的半径．
    标注
    答案
    $\dfrac{4\sqrt 2 }{3}$．
    解析
    本题可设出 $P_1$ 坐标，然后利用对称性表示 $P_2$ 坐标，再利用 $\overrightarrow {P_1F_1}\perp \overrightarrow {P_2F_2}$ 得到 $P_1$ 横纵坐标之间的关系，结合 $P_1$ 在椭圆上求出 $P_1$ 的坐标，从而可求得圆的半径．如图，设圆心在 $y$ 轴上的圆 $C$ 与椭圆 $\dfrac{x^2}{2} + {y^2} = 1$ 相交，${P_1}\left( {{x_1},{y_1}} \right)$，${P_2}\left( {{x_2} , {y_2}} \right)$ 是两个交点，$ {y_1} > 0 $，$ {y_2} > 0 $，${F_1}{P_1}$，${F_2}{P_2}$ 是圆 $C$ 的切线，且 ${F_1}{P_1} \perp {F_2}{P_2}$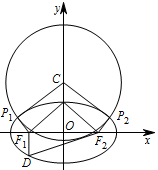．由圆和椭圆的对称性，易知\[{x_2} = - {x_1},{y_1} = {y_2},\left| {{P_1}{P_2}} \right| = 2|{x_1}|.\]由（1）知 ${F_1}\left( { - 1,0} \right)$，${F_2}\left( {1,0} \right)$，根据向量的坐标运算得\[ \overrightarrow {{F_1}{P_1}} = \left( {{x_1} + 1,{y_1}} \right), \overrightarrow {{F_2}{P_2}} = \left( { - {x_1} - 1,{y_1}} \right), \]再由 ${F_1}{P_1} \perp {F_2}{P_2}$ 得 $\overrightarrow {F_1P_1}\cdot \overrightarrow {F_2P_2}= - {\left( {{x_1} + 1} \right)^2} + {y_1}^2=0$，由椭圆方程得\[\dfrac {x_1^2}2+y_1^2=1,\]两式联立并消去 $y_1$ 得\[3x_1^2 + 4{x_1} = 0,\]解得\[{x_1} = - \dfrac{4}{3} 或 {x_1} = 0.\]当 ${x_1} = 0$ 时，${P_1}$，${P_2}$ 重合，此时题设要求的圆不存在．
    当 ${x_1} = - \dfrac{4}{3}$ 时，过 ${P_1}$，${P_2}$ 分别与 ${F_1}{P_1}$，${F_2}{P_2}$ 垂直的直线的交点即为圆心 $C$．
    由 ${F_1}{P_1}$，${F_2}{P_2}$ 是圆 $C$ 的切线，且 ${F_1}{P_1} \perp {F_2}{P_2}$，知 $C{P_2} \perp C{P_1}$，
    又 $|C{P_1}| = |C{P_2}|$，故圆 $C$ 的半径\[\left| {C{P_1}} \right| = \dfrac{\sqrt 2 }{2}\left| {{P_1}{P_2}} \right| = \sqrt 2 \left| {x_1} \right| = \dfrac{4\sqrt 2 }{3}.\]
题目 问题1 答案1 解析1 备注1 问题2 答案2 解析2 备注2
0.115678s