四面体 $ABCD$ 及其三视图如图所示,平行于棱 $AD$,$BC$ 的平面分别交四面体的棱 $AB$,$BD$,$DC$,$CA$ 于点 $E$,$F$,$G$,$H$.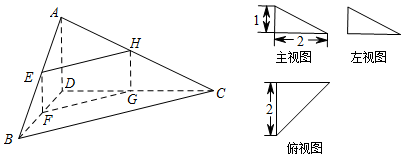

【难度】
【出处】
2014年高考陕西卷(文)
【标注】
-
求四面体 $ABCD$ 的体积;标注答案$ \dfrac{2}{3}$.解析可通过三视图得到 $BD$、$DC$ 和 $AD$ 的长,且 $AD$ 是三棱锥底面上的高.然后求体积即可.由该四面体的三视图可知 $BD \perp DC$,$BD \perp AD$,$AD \perp DC$,$BD = DC = 2$,$AD = 1$,于是 $ AD \perp $ 平面 $BDC$,所以四面体 $ABCD$ 的体积为\[\begin{split}V= \dfrac{1}{3}AD \cdot {S_{\triangle BCD}} = \dfrac{1}{3} \times 1 \times \dfrac{1}{2} \times 2 \times 2 = \dfrac{2}{3}.\end{split}\]
-
证明:四边形 $EFGH$ 是矩形.标注答案略.解析可通过 $BC$ 和 $AD$ 作为桥梁,沟通欲证四边形的四个边.因为 $BC\parallel 平面 EFGH$,
平面 $EFGH \cap 平面 BDC = FG$,
平面 $EFGH \cap 平面 ABC = EH$,
所以 $BC\parallel FG$,$BC\parallel EH$,故 $FG\parallel EH$.
同理 $EF\parallel AD$,$HG\parallel AD$,所以 $EF\parallel HG$.
所以四边形 $EFGH$ 是平行四边形.
又因为 $AD \perp 平面 BDC$,可得 $ AD \perp BC$,
因为 $BC\parallel FG$,$EF\parallel AD$,可知 $ EF \perp FG$,所以四边形 $EFGH$ 是矩形.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2