$f\left(x\right)$ 的极小值为 $ 2 $．

本题考察用导数求函数的极值．函数 $f\left(x\right)$ 的定义域为 $\left(0, + \infty \right)$．
当 $m = {\mathrm{e}}$ 时，$f\left(x\right) = \ln x + \dfrac{{\mathrm{e}}}{x}$，则\[f'\left(x\right) = \dfrac{1}{x} - \dfrac{{\mathrm{e}}}{x^2} = \dfrac{{x - {\mathrm{e}}}}{x^2},\]由此，当 $x \in \left(0,{\mathrm{e}}\right)$ 时，$f'\left(x\right) < 0$，此时 $f\left(x\right)$ 在 $\left(0,{\mathrm{e}}\right)$ 上单调递减；
当 $x \in \left({\mathrm{e}}, + \infty \right)$ 时，$f'\left(x\right) > 0$，此时 $f\left(x\right)$ 在 $\left({\mathrm{e}}, + \infty \right)$ 上单调递增．
于是，当 $x ={\mathrm{ e}}$ 时，$f\left(x\right)$ 取得极小值$f\left({\mathrm{e}}\right) = \ln{\mathrm{ e}} + \dfrac{{\mathrm{e}}}{{\mathrm{e}}} = 2$．
故 $f\left(x\right)$ 的极小值为 $ 2 $．

当 $m > \dfrac{2}{3}$ 时，函数 $g\left(x\right)$ 无零点；
当 $m = \dfrac{2}{3}$ 或 $m \leqslant 0$ 时，函数 $g\left(x\right)$ 有且仅有一个零点；
当 $0 < m < \dfrac{2}{3}$ 时，函数 $g\left(x\right)$ 有两个零点．

算出 $g(x)$ 解析式后，可将问题转化成求直线 $y=m$ 与一个三次函数图象的交点个数问题，继而通过研究三次函数的图象得到结果．由已知得\[g\left(x\right) = f'\left(x\right) - \dfrac{x}{3} = \dfrac{1}{x} - \dfrac{m}{x^2} - \dfrac{x}{3}\left(x > 0\right),\]令 $g\left(x\right) = 0$，得\[m = - \dfrac{1}{3}{x^3} + x\left(x > 0\right),\]设 $\varphi \left(x\right) = - \dfrac{1}{3}{x^3} + x\left(x \geqslant 0\right)$，则\[ \varphi '\left(x\right) = - {x^2} + 1 = - \left(x - 1\right)\left(x + 1\right),\]当 $x \in \left(0,1\right)$ 时，$\varphi '\left(x\right) > 0$，此时 $\varphi \left(x\right)$ 在 $\left(0,1\right)$ 上单调递增；
当 $x \in \left(1, + \infty \right)$ 时，$\varphi '\left(x\right) < 0$，此时 $\varphi \left(x\right)$ 在 $\left(1, + \infty \right)$ 上单调递减．
所以 $x = 1$ 是 $\varphi \left(x\right)$ 的唯一极值点，且是极大值点，因此 $ x=1 $ 也是 $\varphi \left(x\right)$ 的最大值点，于是 $\varphi \left(x\right)$ 的最大值为\[\varphi \left(1\right) = - \dfrac{1}{3} + 1 = \dfrac{2}{3}.\]又 $\varphi \left(0\right) = 0$，结合 $y= \varphi \left(x\right)$ 的图象（如图），可知 $g\left(x\right)$ 的零点情况如下：
① 当 $m > \dfrac{2}{3}$ 时，函数 $g\left(x\right)$ 无零点；
② 当 $m = \dfrac{2}{3}$ 时，函数 $g\left(x\right)$ 有且仅有一个零点；
③ 当 $0 < m < \dfrac{2}{3}$ 时，函数 $g\left(x\right)$ 有两个零点；
④ $m \leqslant 0$ 时，函数 $g\left(x\right)$ 有且只有一个零点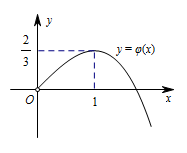．综上，当 $m > \dfrac{2}{3}$ 时，函数 $g\left(x\right)$ 无零点；
当 $m = \dfrac{2}{3}$ 或 $m \leqslant 0$ 时，函数 $g\left(x\right)$ 有且仅有一个零点；
当 $0 < m < \dfrac{2}{3}$ 时，函数 $g\left(x\right)$ 有两个零点．

$\left[\dfrac{1}{4}, + \infty \right)$．

本题可构造函数 $h(x)=f(x)-x$，将问题转化成 $h(x)$ 在 $(0,+\infty)$ 上单减，求 $m$ 的取值范围的问题．对任意 $b > a > 0$，$\dfrac{f\left(b\right) - f\left(a\right)}{b - a} < 1$ 恒成立，等价于 $f\left(b\right) - b < f\left(a\right) - a$ 恒成立，
设 $h\left(x\right) = f\left(x\right) - x = \ln x + \dfrac{m}{x} - x\left(x > 0\right)$，于是等价于 $h\left(x\right)$ 在 $\left(0, + \infty \right)$ 上单调递减．
所以 $ h'\left(x\right) = \dfrac{1}{x} - \dfrac{m}{x^2} - 1 \leqslant 0$ 在 $\left(0, + \infty \right)$ 上恒成立，即\[ m \geqslant - {x^2} + x = - {\left(x - \dfrac{1}{2}\right)^2} + \dfrac{1}{4}\left(x > 0\right)\]恒成立，
只须 $ m \geqslant \dfrac{1}{4}$（对 $m = \dfrac{1}{4},h'\left( x \right) = 0$ 仅在 $x = \dfrac{1}{2}$ 时成立），
故 $ m$ 的取值范围是 $\left[\dfrac{1}{4}, + \infty \right)$．