如图,在平面直角坐标系 $xOy $ 中,${F_1}$,${F_2}$ 分别是椭圆 $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1 \left(a > b > 0\right)$ 的左、右焦点,顶点 $B$ 的坐标为 $\left(0,b\right)$,连接 $B{F_2}$ 并延长交椭圆于点 $A$,过点 $A$ 作 $x$ 轴的垂线交椭圆于另一点 $C$,连接 ${F_1}C$.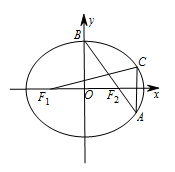

【难度】
【出处】
无
【标注】
-
若点 $C$ 的坐标为 $\left(\dfrac{4}{3},\dfrac{1}{3}\right)$,且 $B{F_2} = \sqrt 2 $,求椭圆的方程;标注答案$\dfrac{x^2}{2} + {y^2} = 1$.解析本题考查椭圆的基本量与方程.将 $C\left(\dfrac 43,\dfrac 13\right)$ 点坐标代入椭圆方程 $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1 \left(a > b > 0\right)$ 得\[\dfrac {16}{9a^2}+\dfrac 1{9b^2}=1,\]又 $a = B{F_2} = \sqrt 2 $,所以可得 $b=1$,所以椭圆方程为 $\dfrac{x^2}{2} + {y^2} = 1$.
-
若 ${F_1}C \perp AB$,求椭圆离心率 $e$ 的值.标注答案$ \dfrac{c}{a} = \dfrac{\sqrt 5 }{5}$.解析本题可先求用 $b,c$ 表示出 $AB$ 方程,然后和椭圆联立求得点 $A$ 坐标,继而得到点 $C$ 坐标,最后利用直线 $AB$ 和 $CF_1$ 斜率相乘得 $-1$ 求得椭圆离心率.将直线 $B{F_2}$ 的方程$\dfrac xc+\dfrac yb=1$ 与椭圆进行联立\[\begin{cases}
\dfrac{x}{c} + \dfrac{y}{b} = 1 ,\\
\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1, \\
\end{cases}\]解得 $A$ 点坐标为\[\left(\dfrac{{2{a^2}c}}{{{a^2} + {c^2}}}, - \dfrac{b^3}{{{a^2} + {c^2}}}\right),\]则根据对称性可得出 $C$ 点坐标为\[\left(\dfrac{{2{a^2}c}}{{{a^2} + {c^2}}}, \dfrac{b^3}{{{a^2} + {c^2}}}\right),\]所以直线 $F_1C$ 的斜率为\[{k_{{F_1}C}} = \dfrac{{\dfrac{b^3}{{{a^2} + {c^2}}}}}{{\dfrac{{2{a^2}c}}{{{a^2} + {c^2}}} + c}} = \dfrac{b^3}{{3{a^2}c + {c^3}}},\]又 ${k_{AB}} = - \dfrac{b}{c}$,由 ${F_1}C \perp AB$得\[\dfrac{b^3}{{3{a^2}c + {c^3}}} \cdot \left( - \dfrac{b}{c}\right) = - 1,\]即 ${b^4} = 3{a^2}{c^2} + {c^4}$,结合 $b^2=a^2-c^2$得\[{\left({a^2} - {c^2}\right)^2} = 3{a^2}{c^2} + {c^4},\]化简得 $e = \dfrac{c}{a} = \dfrac{\sqrt 5 }{5}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2