如图,在直棱柱 $ABC - {A_1}{B_1}{C_1}$ 中,$\angle BAC = 90^\circ ,AB = AC = \sqrt 2 ,A{A_1} = 3$,$D$ 是 $BC$ 的中点,点 $E$ 在棱 $B{B_1}$ 上运动.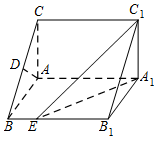

【难度】
【出处】
2013年高考湖南卷(文)
【标注】
-
证明:$AD \perp {C_1}E$;标注答案略解析可通过证明 $AD\perp 面 BB_1C_1C$ 来证明 $AD\perp C_1E$.因为 $AB = AC$,$D$ 是 $BC$ 的中点,所以\[AD \perp BC ,\quad \cdots \cdots ① \]又在直三棱柱 $ABC - {A_1}{B_1}{C_1}$ 中,$B{B_1} \perp $ 平面 $ABC$,
而 $AD \subset $ 平面 $ABC$,所以\[AD \perp B{B_1}. \quad \cdots \cdots ② \]由 ①②,得$AD \perp $ 平面 $B{B_1}{C_1}C$,
由点 $E$ 在棱 $B{B_1}$ 上运动,得 ${C_1}E \subset $ 平面 $B{B_1}{C_1}C$,
所以$AD \perp {C_1}E$. -
当异面直线 $AC,{C_1}E$ 所成的角为 $60^\circ $ 时,求三棱锥 ${C_1} - {A_1}{B_1}E$ 的体积.标注答案$\dfrac{2}{3}$解析先通过异面直线 $AC,{C_1}E$ 所成的角为 $60^\circ $ 求出 $B_1E$ 长,然后再求三棱锥体积.因为 $AC\parallel {A_1}{C_1}$,所以 $\angle {A_1}{C_1}E$ 是异面直线 $AC,{C_1}E$ 所成的角.
由题意知 $\angle {A_1}{C_1}E = 60^\circ $.
因为 $\angle {B_1}{A_1}{C_1} = \angle BAC = 90^\circ $,所以 ${A_1}{C_1} \perp {A_1}{B_1}$.
又 $A{A_1} \perp {A_1}{C_1}$,从而${A_1}{C_1} \perp $ 平面 ${A_1}AB{B_1}$.
于是${A_1}{C_1} \perp {A_1}E$,故\[{C_1}E = \dfrac{{{A_1}{C_1}}}{\cos 60^\circ } = 2\sqrt 2 .\]又 ${B_1}{C_1} = \sqrt {{A_1}C_1^2 + {A_1}B_1^2} = 2$,所以\[{B_1}E = \sqrt {{C_1}{E^2} - {B_1}C_1^2} = 2.\]从而\[\begin{split}{V_{三棱锥{C_1} - {A_1}{B_1}E}} &= \dfrac{1}{3}{S_{\triangle {A_1}{B_1}E}} \cdot {A_1}{C_1} \\&= \dfrac{1}{3} \times \dfrac{1}{2} \times 2 \times \sqrt 2 \times \sqrt 2 \\&= \dfrac{2}{3}.\end{split}\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2