如图，在四棱锥 $P - ABCD$ 中，$PA \perp $ 平面 $ABCD$，$AB = BC = 2$，$AD = CD = \sqrt 7 $，$PA = \sqrt 3 $，$\angle ABC = 120^\circ $，$G$ 为线段 $PC$ 上的点．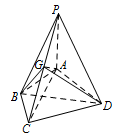
【难度】
【出处】
2013年高考浙江卷（文）
【标注】
-
证明：$BD \perp $ 平面 $APC$；标注答案略解析本题需要借助边的关系来求垂直．设点 $O$ 为 $AC$，$BD$ 的交点．
由 $AB = BC$，$AD = CD$，得 $BD$ 是线段 $AC$ 的中垂线．
所以 $O$ 为 $AC$ 的中点，$BD \perp AC$．
又因为 $PA \perp $ 平面 $ABCD$，$BD \subset $ 平面 $ABCD$，所以 $PA \perp BD$．
所以 $BD \perp $ 平面 $APC$．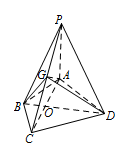
-
若 $G$ 为 $PC$ 的中点，求 $DG$ 与平面 $APC$ 所成的角的正切值；标注答案$\dfrac{4\sqrt 3 }{3}$解析在第一问证明的基础上构造出线面角，然后求值即可．连接 $OG$．由（1）可知，$OD \perp $ 平面 $APC$，则 $DG$ 在平面 $APC$ 内的射影为 $OG$，所以 $\angle OGD$ 是 $DG$ 与平面 $APC$ 所成的角．
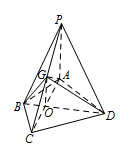由题意得\[OG = \dfrac{1}{2}PA = \dfrac{\sqrt 3 }{2}.\]在 $\triangle ABC$ 中，由余弦定理可得\[\begin{split}AC &= \sqrt {A{B^2} + B{C^2} - 2AB \cdot BC \cdot \cos \angle ABC} \\ & = \sqrt {4 + 4 - 2 \times 2 \times 2 \times \left( { - \dfrac{1}{2}} \right)} \\ & = 2\sqrt 3, \end{split}\]所以\[OC = \dfrac{1}{2}AC = \sqrt 3 .\]在直角 $\triangle OCD$ 中，\[OD = \sqrt {C{D^2} - O{C^2}} = \sqrt {7 - 3} = 2.\]在直角 $\triangle OGD$ 中，\[\tan \angle OGD = \dfrac{OD}{OG} = \dfrac{4\sqrt 3 }{3},\]所以 $ DG $ 与平面 $ APC $ 所成的角的正切值为 $\dfrac{4\sqrt 3 }{3}$． -
若 $G$ 满足 $PC \perp $ 平面 $BGD$，求 $\dfrac{PG}{GC}$ 的值．标注答案$ \dfrac{3}{2}$解析利用垂直构造相等的条件，解方程即得．因为 $PC \perp $ 平面 $BGD$，$OG \subset $ 平面 $BGD$，所以 $PC \perp OG$．
在直角 $\triangle PAC$ 中，\[PC = \sqrt {P{A^2} + A{C^2}} = \sqrt {3 + 12} = \sqrt {15} ,\]所以\[GC = \dfrac{AC \cdot OC}{PC} = \dfrac{2\sqrt 3 \times \sqrt 3 }{{\sqrt {15} }} = \dfrac{{2\sqrt {15} }}{5},\]从而 $PG = \dfrac{{3\sqrt {15} }}{5}$，所以\[\dfrac{PG}{GC} = \dfrac{3}{2}.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
