已知抛物线 $C$ 的顶点为 $O\left(0,0\right)$,焦点为 $F\left(0,1\right)$.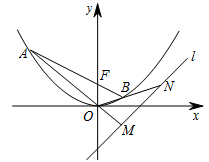

【难度】
【出处】
2013年高考浙江卷(文)
【标注】
-
求抛物线 $C$ 的方程;标注答案${x^2} = 4y$解析利用焦点坐标直接确定基本量即可.由题意可设抛物线 $C$ 的方程为 ${x^2} = 2py \left(p > 0 \right)$,则 $\dfrac{p}{2} = 1$,所以抛物线 $C$ 的方程为 ${x^2} = 4y$.
-
过点 $F$ 作直线交抛物线 $C$ 于 $A,B$ 两点,若直线 $AO,BO$ 分别交直线 $l:y = x - 2$ 于 $M,N$ 两点,求 $ \left|MN \right|$ 的最小值.标注答案$\dfrac{8}{5}\sqrt 2 $解析本题的关键在于把 $|MN|$ 用一个变量表示出来,结合韦达定理求解.设 $A \left({x_1},{y_1} \right),B \left({x_2},{y_2} \right)$,直线 $AB$ 的方程为 $y = kx + 1$.
由 ${\begin{cases}
y = kx + 1 ,\\
{x^2} = 4y ,\\
\end{cases}}$ 消去 $y$,整理得\[{x^2} - 4kx - 4 = 0,\]所以\[\begin{split}{x_1} + {x_2} &= 4k,{x_1}{x_2} &= - 4.\end{split}\]从而\[\left|{x_1} - {x_2} \right| = 4\sqrt {{k^2} + 1} .\]由 ${\begin{cases}y = \dfrac{y_1}{x_1}x, \\
y = x - 2, \\
\end{cases}}$ 解得,点 $M$ 的横坐标\[{x_M} = \dfrac{{2{x_1}}}{{{x_1} - {y_1}}}= \dfrac{{2{x_1}}}{{{x_1} - \dfrac{x_1^2}{4}}} = \dfrac{8}{{4 - {x_1}}}.\]同理,点 $N$ 的横坐标 ${x_N} = \dfrac{8}{{4 - {x_2}}}$.由弦长公式可得\[\begin{split} \left|MN \right| & = \sqrt 2 \left|{x_M} - {x_N}\right| \\ & = \sqrt 2 \left| {\dfrac{8}{{4 - {x_1}}} - \dfrac{8}{{4 - {x_2}}}} \right| \\ & = 8\sqrt 2 \left| {\dfrac{{{x_1} - {x_2}}}{{{x_1}{x_2} - 4\left({x_1} + {x_2}\right) + 16}}} \right|\\ & = \dfrac{{8\sqrt 2 \sqrt {{k^2} + 1} }}{{\left| {4k - 3} \right|}}.\end{split}\]令 $4k - 3 = t,t \ne 0$,则 $k = \dfrac{t + 3}{4}$.当 $t > 0$ 时,\[\begin{split}\left| {MN} \right| &= 2\sqrt 2 \sqrt {\dfrac{25}{t^2} + \dfrac{6}{t} + 1} \\& > 2\sqrt 2 .\end{split}\]当 $t < 0$ 时,\[\begin{split} \left|MN \right| &= 2\sqrt 2 \sqrt {{{\left( {\dfrac{5}{t} + \dfrac{3}{5}} \right)}^2} + \dfrac{16}{25}} \\& \geqslant \dfrac{8}{5}\sqrt 2 .\end{split}\]综上所述,当 $t = - \dfrac{25}{3}$,即 $k = - \dfrac{4}{3}$ 时,$\left|MN\right|$ 的最小值是 $\dfrac{8}{5}\sqrt 2 $.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2