如图,某地质队自水平地面 $A$,$B$,$C$ 三处垂直向地下钻探,自 $A$ 点向下钻到 ${A_1}$ 处发现矿藏,再继续下钻到 ${A_2}$ 处后下面已无矿,从而得到在 $A$ 处正下方的矿层厚度为 ${A_1}{A_2} = {d_1}$,同样可得在 $B$,$C$ 处正下方的矿层厚度分别为 ${B_1}{B_2} = {d_2}$,${C_1}{C_2} = {d_3}$,且 ${d_1} < {d_2} < {d_3}$,过 $AB$,$AC$ 的中点 $M$,$N$ 且与直线 $A{A_2}$ 平行的平面截多面体 ${A_1}{B_1}{C_1} - {A_2}{B_2}{C_2}$ 所得的截面 $DEFG$ 为该多面体的一个中截面,其面积记为 ${S_中}$.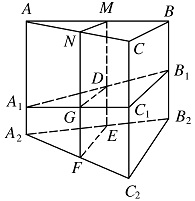

【难度】
【出处】
2013年高考湖北卷(文)
【标注】
-
证明:中截面 $DEFG$ 是梯形.标注答案略解析需要证明 $DE$ 和 $FG$ 平行且不相等,要用到线面平行的性质定理,以及棱柱的性质.依题意 ${A_1}{A_2} \perp 平面 ABC$,${B_1}{B_2} \perp 平面 ABC$,${C_1}{C_2} \perp 平面 ABC$,所以 ${A_1}{A_2}\parallel {B_1}{B_2}\parallel {C_1}{C_2}$.
又 ${A_1}{A_2} = {d_1}$,${B_1}{B_2} = {d_2}$,${C_1}{C_2} = {d_3}$,且 ${d_1} < {d_2} < {d_3}$,所以四边形 ${A_1}{A_2}{B_2}{B_1}$,${A_1}{A_2}{C_2}{C_1}$ 均是梯形.
由 $A{A_2}\parallel 平面 MEFN$,$A{A_2} \subset 平面 A{A_2}{B_2}B$,且平面 $A{A_2}{B_2}B \cap 平面 MEFN = ME$,可得 $A{A_2}\parallel ME$,即 ${A_1}{A_2}\parallel DE$.
同理可证 ${A_1}{A_2}\parallel FG$,所以 $DE\parallel FG$.
又点 $M$,$N$ 分别为 $AB$,$AC$ 的中点,则点 $D$,$E$,$F$,$G$ 分别为 ${A_1}{B_1}$,${A_2}{B_2}$,${A_2}{C_2}$,${A_1}{C_1}$ 的中点,
即 $DE$,$FG$ 分别为梯形 ${A_1}{A_2}{B_2}{B_1}$,${A_1}{A_2}{C_2}{C_1}$ 的中位线,因此\[\begin{split}DE &= \dfrac{1}{2}\left({A_1}{A_2} + {B_1}{B_2}\right) \\&= \dfrac{1}{2}\left({d_1} + {d_2}\right), \\ FG &= \dfrac{1}{2}\left({A_1}{A_2} + {C_1}{C_2}\right) \\&= \dfrac{1}{2}\left({d_1} + {d_3}\right),\end{split}\]而 ${d_1} < {d_2} < {d_3}$,故 $DE < FG$,所以中截面 $DEFG$ 是梯形. -
在 $\triangle ABC$ 中,记 $BC = a$,$BC$ 边上的高为 $h$,面积为 $S$.在估测三角形 $ABC$ 区域内正下方的矿藏储量(即多面体 ${A_1}{B_1}{C_1} - {A_2}{B_2}{C_2}$ 的体积 $V$)时,可用近似公式 ${V_估} = {S_中} \cdot h$ 来估算.已知 $V = \dfrac{1}{3}\left({d_1} + {d_2} + {d_3}\right)S$,试判断 ${V_估}$ 与 $V$ 的大小关系,并加以证明.标注答案${V_估} < V$,证明略解析先把 $V_估$ 和 $V$ 都表达出来,然后作差比较大小.${V_估} < V$.证明如下:
由 ${A_1}{A_2} \perp 平面 ABC$,$MN \subset 平面 ABC$,可得 ${A_1}{A_2} \perp MN$.
而 $EM\parallel {A_1}{A_2}$,所以 $EM \perp MN$,同理可得 $FN \perp MN$.
由 $MN$ 是 $\triangle ABC$ 的中位线,可得\[MN = \dfrac{1}{2}BC = \dfrac{1}{2}a,\]即为梯形 $DEFG$ 的高.因此\[\begin{split}{S_中} &= {S_{梯形DEFG}} \\&= \dfrac{1}{2}\left( {\dfrac{{{d_1} + {d_2}}}{2} + \dfrac{{{d_1} + {d_3}}}{2}} \right) \cdot \dfrac{a}{2} \\&= \dfrac{a}{8}\left(2{d_1} + {d_2} + {d_3}\right),\end{split}\]所以\[\begin{split}{V_估} &= {S_中} \cdot h \\&= \dfrac{ah}{8}\left(2{d_1} + {d_2} + {d_3}\right).\end{split}\]又 $S = \dfrac{1}{2}ah$,所以\[\begin{split} V &= \dfrac{1}{3}\left({d_1} + {d_2} + {d_3}\right)S \\ & = \dfrac{ah}{6}\left({d_1} + {d_2} + {d_3}\right) .\end{split} \]于是\[\begin{split} V-{V_估} &= \dfrac{ah}{6}\left({d_1}+{d_2}+{d_3}\right)- \dfrac{ah}{8}\left(2{d_1} + {d_2} + {d_3}\right) \\ & = \dfrac{ah}{24}\left[ {\left({d_2} - {d_1}\right) + \left({d_3} - {d_1}\right)} \right].\end{split} \]由 ${d_1} < {d_2} < {d_3}$,得\[{d_2} - {d_1} > 0,{d_3} - {d_1} > 0,\]故 ${V_估} < V$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2