在平面直角坐标系 $ xOy $ 中,将从点 $ M $ 出发沿纵、横方向到达点 $ N $ 的任一路径称为 $ M $ 到 $ N $ 的一条“$ L $ 路径”.如图所示的路径 $M{M_1}M{}_2{M_3}N$ 与路径 $M{N_1}N$ 都是 $ M $ 到 $ N $ 的“$ L $ 路径”.某地有三个新建的居民区,分别位于平面 $ xOy $ 内三点 $A\left(3,20\right)$,$B\left( - 10,0\right)$,$C\left(14,0\right)$ 处.现计划在 $ x $ 轴上方区域(包含 $ x $ 轴)内的某一点 $ P $ 处修建一个文化中心.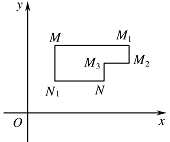

【难度】
【出处】
2013年高考湖南卷(理)
【标注】
-
写出点 $ P $ 到居民区 $ A $ 的“$ L $ 路径”长度最小值的表达式(不要求证明);标注答案$ |x - 3| + |y - 20|$,$y \geqslant 0,x \in {\mathbb{R}}$解析本题考查实际应用问题,认真阅读题意可以直接写出答案,注意定义域.设点 $ P $ 的坐标为 $ \left(x,y\right) $,点 $ P $ 到居民区 $ A $ 的“$ L $ 路径”长度最小值为 $ |x - 3| + |y - 20|$,$y \geqslant 0,x \in {\mathbb{R}}$.
-
若以原点 $ O $ 为圆心,半径为 $ 1 $ 的圆的内部是保护区,“$ L $ 路径”不能进入保护区,请确定点 $ P $ 的位置,使其到三个居民区的“$ L $ 路径”长度之和最小.标注答案当点 $ P\left(x,y\right) $ 在点 $ P\left(3,1\right) $ 处,点 $ P $ 到 $ A $,$ B $,$ C $ 三点的“$ L $ 路径”长度之和 $ d $ 有最小值,为 $ 45 $解析本题要先准确的理解题意,转化为数学问题,然后求解.情况不唯一时,注意合理的进行分类讨论.点 $ P $ 到 $ A $,$ B $,$ C $ 三点的“$ L $ 路径”长度之和的最小值 $ d =h+v$,其中 $ h $ 表示水平距离之和的最小值,$ v $ 表示垂直距离之和的最小值,且 $ h $ 和 $ v $ 互不影响.
显然当 $ y=1 $ 时,$ v = 20+1=21 $;
显然当 $ x \in \left[ - 10,14\right] $ 时,水平距离之和\[h=x - \left(-10\right) + 14 - x + |x-3| \geqslant 24,\]且当 $ x=3 $ 时,$ h=24 $.
因此,当 $ P\left(3,1\right) $ 时,$ d=21+24=45 $.
所以,当点 $ P\left(x,y\right) $ 在点 $ P\left(3,1\right) $ 处,点 $ P $ 到 $ A $,$ B $,$ C $ 三点的“$ L $ 路径”长度之和 $ d $ 的最小值为 $ 45 $.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2