查看数据源：599165c62bfec200011e0e8a
如图，在四棱锥 $P - ABCD$ 中，$PD \perp 平面 ABCD$，$AB\parallel DC$，$AB \perp AD$，$BC = 5$，$DC = 3$，$AD = 4$，$\angle PAD = 60^\circ $．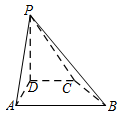 
【难度】
【出处】
2013年高考福建卷（文）
【标注】
  1. 当正视方向与向量 $\overrightarrow {AD} $ 的方向相同时，画出四棱锥 $P - ABCD$ 的正视图（要求标出尺寸，并写出演算过程）；
    标注
    答案
    略
    解析
    本题考查三视图的画法．在梯形 $ABCD$ 中，如图1，过点 $C$ 作 $CE \perp AB$，垂足为 $E$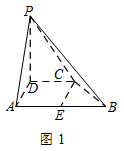．由已知得，四边形 $ADCE$ 为矩形，\[AE = CD = 3,\]在 ${\mathrm{Rt}} \triangle BEC$ 中，\[BC = 5,CE = 4,\]由勾股定理得\[BE = 3,\]从而\[AB = 6.\]又由 $PD \perp 平面 ABCD$，得 $PD \perp AD$，从而在 ${\mathrm{Rt}} \triangle PDA$ 中，由 $AD = 4$，$\angle PAD = 60^\circ $，得\[PD = 4\sqrt 3 .\]于是正视图如图2所示．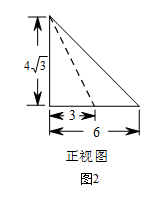
  2. 若 $M$ 为 $PA$ 的中点，求证：$DM\parallel 平面 PBC$；
    标注
    答案
    略
    解析
    在面上，找一条与 $DM$ 平行的直线即可．解法一：
    如图3，取 $PB$ 的中点 $N$，连接 $MN$，$CN$，$MD$．在 $\triangle PAB$ 中，
    因为 $M、N$ 分别是 $PA、PB$ 的中点，所以 $MN\parallel AB$，$MN = \dfrac{1}{2}AB = 3$，
    又 $CD\parallel AB$，$CD = 3$，
    所以 $MN\parallel CD$，$MN = CD$，所以四边形 $MNCD$ 为平行四边形，于是 $DM\parallel CN$．
    又 $DM \not\subset 平面 PBC$，$CN \subset 平面 PBC$，
    所以 $DM\parallel 平面 PBC$．
    解法二：
    如图4，取 $AB$ 的中点 $E$，连接 $ME$，$DE$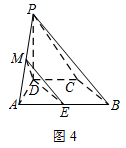．在梯形 $ABCD$ 中，$BE\parallel CD$，且 $BE = CD$，
    所以四边形 $BCDE$ 为平行四边形，因此 $DE\parallel BC$．
    又 $DE \not\subset 平面 PBC$，$BC \subset 平面 PBC$，
    所以 $DE\parallel 平面 PBC$，
    又在 $\triangle PAB$ 中，$ME\parallel PB$，
    $ME \not\subset 平面 PBC$，$PB \subset 平面 PBC$，
    所以 $ME\parallel 平面 PBC$．
    又 $DE \cap ME = E$，所以平面 $DME\parallel 平面 PBC$，
    又 $DM \subset 平面 DME$，所以 $DM\parallel 平面 PBC$．
  3. 求三棱锥 $D - PBC$ 的体积．
    标注
    答案
    $ 8\sqrt 3$
    解析
    本题考查三棱锥的体积求法，确定合适的顶点是解决问题的关键．由三棱锥的特点可得\[{V_{D - PBC}} = {V_{P - DBC}} = \dfrac{1}{3}{S_{\triangle DBC}} \cdot PD,\]又\[{S_{\triangle DBC}} = 6, PD = 4\sqrt 3 ,\]所以\[{V_{D - PBC}} = 8\sqrt 3 .\]
题目 问题1 答案1 解析1 备注1 问题2 答案2 解析2 备注2 问题3 答案3 解析3 备注3
0.182644s