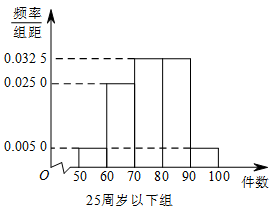
某工厂有 $ 25 $ 周岁以上(含 $ 25 $ 周岁)工人 $ 300 $ 名,$ 25 $ 周岁以下工人 $ 200 $ 名.为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了 $ 100 $ 名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在" $ 25 $ 周岁以上(含 $ 25 $ 周岁)"和" $ 25 $ 周岁以下"分为两组,再将两组工人的日平均生产件数分成 $ 5 $ 组:$\left[ {50,60} \right)$,$\left[ {60,70} \right) $,$\left[ {70,80} \right)$,$\left[ {80,90} \right)$,$\left[ {90,100} \right]$ 分别加以统计,得到如图所示的频率分布直方图.
附:${\chi ^2} = \dfrac{{n{{\left({n_{11}}{n_{22}} - {n_{12}}{n_{21}}\right)}^2}}}{{{n_{1 + }}{n_{2 + }}{n_{ + 1}}{n_{ + 2}}}}$\[ \begin{array}{|c|c|c|c|c|} \hline
P\left(\chi ^2 \geqslant k\right)& 0.100 & 0.050 & 0.010 & 0.001 \\ \hline
k & 2.706 & 3.841 & 6.635 & 10.828 \\ \hline \end{array} \](注:此公式也可以写成 ${K^2} = \dfrac{{n{{\left(ad - bc\right)}^2}}}{\left(a + b\right)\left(c + d\right)\left(a + c\right)\left(b + d\right)}$)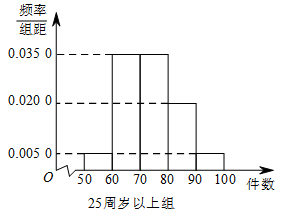
附:${\chi ^2} = \dfrac{{n{{\left({n_{11}}{n_{22}} - {n_{12}}{n_{21}}\right)}^2}}}{{{n_{1 + }}{n_{2 + }}{n_{ + 1}}{n_{ + 2}}}}$\[ \begin{array}{|c|c|c|c|c|} \hline
P\left(\chi ^2 \geqslant k\right)& 0.100 & 0.050 & 0.010 & 0.001 \\ \hline
k & 2.706 & 3.841 & 6.635 & 10.828 \\ \hline \end{array} \](注:此公式也可以写成 ${K^2} = \dfrac{{n{{\left(ad - bc\right)}^2}}}{\left(a + b\right)\left(c + d\right)\left(a + c\right)\left(b + d\right)}$)


【难度】
【出处】
2013年高考福建卷(文)
【标注】
-
从样本中日平均生产件数不足 $ 60 $ 件的工人中随机抽取 $ 2 $ 人,求至少抽到一名" $ 25 $ 周岁以下组"工人的概率;标注答案$ \dfrac{7}{10}$解析本题考查古典概型,将基本事件空间找出,并找出符合题意的事件空间即可.由已知得,样本中有 $ 25 $ 周岁以上组工人 $ 60 $ 名,$ 25 $ 周岁以下组工人 $ 40 $ 名.
所以,样本中日平均生产件数不足 $ 60 $ 件的工人中,
$ 25 $ 周岁以上组工人有 $60 \times 0.05 = 3$(人),记为 ${A_1},{A_2},{A_3}$;
$ 25 $ 周岁以下组工人有 $40 \times 0.05 = 2$(人),记为 ${B_1},{B_2}$.
从中随机抽取 $ 2 $ 名工人,所有的可能结果共有 $ 10 $ 种,它们是:\[\left({A_1},{A_2}\right),\left({A_1},{A_3}\right),\left({A_2},{A_3}\right),\left({A_1},{B_1}\right),\left({A_1},{B_2}\right),\\ \left({A_2},{B_1}\right),\left({A_2},{B_2}\right),\left({A_3},{B_1}\right),\left({A_3},{B_2}\right),\left({B_1},{B_2}\right).\]其中,至少有 $ 1 $ 名" $ 25 $ 周岁以下组"工人的可能结果共有 $ 7 $ 种,它们是:\[\left({A_1},{B_1}\right),\left({A_1},{B_2}\right),\left({A_2},{B_1}\right),\\ \left({A_2},{B_2}\right),\left({A_3},{B_1}\right),\left({A_3},{B_2}\right),\left({B_1},{B_2}\right),\]故所求的概率\[P = \dfrac{7}{10}.\] -
规定日平均生产件数不少于 $ 80 $ 件者为"生产能手",请你根据已知条件完成 $2 \times 2$ 列联表,并判断是否有 $90\% $ 的把握认为"生产能手与工人所在的年龄组有关"?标注答案没有 $90\% $ 的把握认为"生产能手与工人所在的年龄组有关"解析本题考查独立性检验,根据题意列出 $2\times2$ 的列联表,再利用公式求解即可.由频率分布直方图可知,在抽取的 $ 100 $ 名工人中,
" $ 25 $ 周岁以上组"中的生产能手 $60 \times 0.25 = 15$(人),
" $ 25 $ 周岁以下组"中的生产能手 $40 \times 0.375 = 15$(人),
据此可得 $2 \times 2$ 列联表如下:\begin{array}{|c|c|c|c|} \hline & 生产能手 & 非生产能手 & 合计 \\ \hline 25周岁以上组 & 15 & 45 & 60 \\ \hline 25周岁以下组 & 15 & 25 & 40 \\ \hline 合计 & 30 & 70 & 100 \\ \hline \end{array}所以得\[\begin{split}{K^2} &= \dfrac{{n{{\left(ad - bc\right)}^2}}}{\left(a + b\right)\left(c + d\right)\left(a + c\right)\left(b + d\right)} \\& = \dfrac{{100 \times {{\left(15 \times 25 - 15 \times 45\right)}^2}}}{60 \times 40 \times 30 \times 70} \\& = \dfrac{25}{14} \approx 1.79.\end{split}\]因为 $1.79 < 2.706$,所以没有 $90\% $ 的把握认为"生产能手与工人所在的年龄组有关".
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2