如图,抛物线 $E:{y^2} = 4x$ 的焦点为 $F$,准线 $l$ 与 $x$ 轴的交点为 $A$.点 $C$ 在抛物线 $E$ 上,以 $C$ 为圆心,$|CO|$ 为半径作圆,设圆 $C$ 与准线 $l$ 交于不同的两点 $M$,$N$.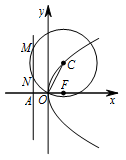

【难度】
【出处】
2013年高考福建卷(文)
【标注】
-
若点 $C$ 的纵坐标为 $ 2 $,求 $|MN|$;标注答案$ 2$解析本题考查圆的弦长公式,圆的弦长通常根据圆心与直线的距离结合半径长解决.抛物线 ${y^2} = 4x$ 的准线 $l$ 的方程为\[x = - 1.\]由点 $C$ 的纵坐标为 $ 2 $,得点 $C$ 的坐标为 $\left(1,2\right)$,所以点 $C$ 到准线 $l$ 的距离\[d = 2.\]又 $|CO| = \sqrt 5 $,则根据圆的弦长公式,可得\[\begin{split}|MN| &= 2\sqrt {|CO|^2 - {d^2}} \\&= 2\sqrt {5 - 4} \\&= 2.\end{split}\]
-
若 $|AF{|^2} = |AM| \cdot |AN|$,求圆 $C$ 的半径.标注答案$\dfrac{{\sqrt {33} }}{2}$解析求出 $|AF|$ 的长度,将题中条件 $|AF{|^2} = |AM| \cdot |AN|$ 转化为 $M,N$ 的纵坐标的乘积关系是解决本题的关键.设 $C\left( {\dfrac{y_0^2}{4},{y_0}} \right)$,则圆 $C$ 的方程为\[\left( {x - \dfrac{y_0^2}{4}} \right) ^2+ {\left(y - {y_0}\right)^2} = \dfrac{y_0^4}{16} + y_0^2,\]即\[{x^2} - \dfrac{y_0^2}{2}x + {y^2} - 2{y_0}y = 0.\]由 $x = - 1$,得\[{y^2} - 2{y_0}y + 1 + \frac{y_0^2}{2} = 0,\]设 $M\left( - 1,{y_1}\right)$,$N\left( - 1,{y_2}\right)$,则\[{\begin{cases}
\Delta = 4y_0^2 - 4\left( {1 + \dfrac{y_0^2}{2}} \right) = 2y_0^2 - 4 > 0, \\
{y_1}{y_2} = \dfrac{y_0^2}{2} + 1. \\
\end{cases}}\]由 $|AF|^2 = |AM| \cdot |AN|$,得 $|{y_1}{y_2}| = 4$,所以\[\dfrac{y_0^2}{2} + 1 = 4,\]解得\[{y_0} = \pm \sqrt 6 ,\]此时 $\Delta > 0$,所以圆心 $C$ 的坐标为\[\left( {\dfrac{3}{2},\sqrt 6 } \right)或\left( {\frac{3}{2}, - \sqrt 6 } \right),\]从而可得点 $C$ 与点 $O$ 的距离为\[|CO{|^2} = \dfrac{33}{4},|CO| = \dfrac{{\sqrt {33} }}{2},\]即圆 $C$ 的半径为 $\dfrac{{\sqrt {33} }}{2}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2