查看数据源：599165c62bfec200011e0e8d
如图，在等腰直角 $\triangle OPQ$ 中，$\angle POQ = 90^\circ$，$OP = 2\sqrt 2 $，点 $M$ 在线段 $PQ$ 上．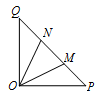 
【难度】
【出处】
2013年高考福建卷（文）
【标注】
  1. 若 $OM = \sqrt 5 $，求 $PM$ 的长；
    标注
    答案
    $MP = 1$ 或 $MP = 3$
    解析
    三角形 $OMP$ 中，已知两边一角，可用余弦定理求第三边．在 $\triangle OMP$ 中，$\angle OPM = 45^\circ$，$OM = \sqrt 5 $，$OP = 2\sqrt 2 $，
    由余弦定理得，\[O{M^2} = O{P^2} + M{P^2} - 2OP \cdot MP \cdot \cos 45^\circ ,\]得\[M{P^2} - 4MP + 3 = 0,\]解得\[MP = 1 或 MP = 3.\]
  2. 若点 $N$ 在线段 $MQ$ 上，且 $\angle MON = 30^\circ $，问：当 $\angle POM$ 取何值时，$\triangle OMN$ 的面积最小？并求出面积的最小值．
    标注
    答案
    $\angle POM = 30^\circ $ 时，$\triangle OMN$ 的面积最小，为 $8 - 4\sqrt 3 $
    解析
    本题中的主动变量为 $\angle POM$，因此，可以考虑将三角形面积中的未知量全用其表示．设 $\angle POM = \alpha $，$0^\circ \leqslant \alpha \leqslant 60^\circ $，
    在 $\triangle OMP$ 中，由正弦定理，得\[\dfrac{OM}{\sin \angle OPM} = \dfrac{OP}{\sin \angle OMP},\]由诱导公式可得\[OM = \dfrac{OP\sin 45^\circ }{\sin \left(45^\circ + \alpha \right)},\]同理\[ON = \dfrac{OP\sin 45^\circ }{\sin \left(75^\circ + \alpha \right)}.\]故\[\begin{split}{S_{\triangle OMN}} &\overset{\left[a\right]}= \dfrac{1}{2} \cdot OM \cdot ON \cdot \sin \angle MON \\&= \dfrac{1}{4} \times \dfrac{{O{P^2}{{\sin }^2}45^\circ }}{\sin \left(45^\circ + \alpha \right)\sin \left(75^\circ + \alpha \right)} \\&\overset{\left[b\right]}= \dfrac{1}{{\sin \left(45^\circ + \alpha \right) \left[ {\dfrac{\sqrt 3 }{2}\sin \left(45^\circ + \alpha \right) + \dfrac{1}{2}\cos \left(45^\circ + \alpha \right)} \right]}} \\&= \dfrac{1}{{\dfrac{\sqrt 3 }{2}{{\sin }^2}\left( {{{45}^ \circ } + \alpha } \right){ + }\dfrac{1}{2}\sin \left( {{{45}^ \circ }{ + }\alpha } \right)\cos \left( {{{45}^ \circ } + \alpha } \right)}} \\&\overset{\left[c\right]}= \dfrac{1}{{\dfrac{\sqrt 3 }{4}\left[ {1 - \cos \left(90^\circ + 2\alpha \right)} \right] + \dfrac{1}{4}\sin \left(90^\circ + 2\alpha \right)}} \\&\overset{\left[d\right]}= \dfrac{1}{{\dfrac{\sqrt 3 }{4} + \dfrac{\sqrt 3 }{4}\sin 2\alpha + \dfrac{1}{4}\cos 2\alpha }} \\&\overset{\left[e\right]}= \dfrac{1}{{\dfrac{\sqrt 3 }{4} + \dfrac{1}{2}\sin \left(2\alpha + 30^\circ \right)}}.\end{split}\]（推导中用到：[a][b][c][d][e]）因为\[0^\circ \leqslant \alpha \leqslant 60^\circ ,30^\circ \leqslant 2\alpha + 30^\circ \leqslant 150^\circ ,\]所以当 $\alpha = 30^\circ $ 时，$\sin \left(2\alpha + 30^\circ \right)$ 的最大值为 $ 1 $，此时 $\triangle OMN$ 的面积取到最小值，
    即 $\angle POM = 30^\circ $ 时，$\triangle OMN$ 的面积的最小值为 $8 - 4\sqrt 3 $．
题目 问题1 答案1 解析1 备注1 问题2 答案2 解析2 备注2
0.116805s