一辆小客车上有 $5$ 个座位，其座位号为 $1$，$2$，$3$，$4$，$5$．乘客 $P_1$，$P_2$，$P_3$，$P_4$，$P_5$ 的座位号分别为 $1$，$2$，$3$，$4$，$5$，他们按照座位号从小到大的顺序先后上车．乘客 $P_1$ 因身体原因没有坐自己的 $1$ 号座位，这时司机要求余下的乘客按以下规则就座：如果自己的座位空着，就只能坐自己的座位；如果自己的座位已有乘客就座，就在这 $5$ 个座位的剩余空位中任意选择座位．
【难度】
【出处】
2015年高考四川卷（文）
【标注】
-
若乘客 $P_1$ 坐到了 $3$ 号座位，其他乘客按规则就座，则此时共有 $4$ 种坐法．下表给出了其中两种坐法，请填入余下两种坐法（将乘客就座的座位号填入表中空格处）；
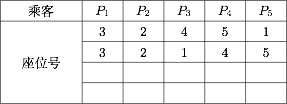标注答案余下两种坐法如下表所示：
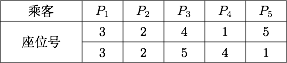解析按照规则逐一试填即可得出答案．按规则，$P_2$ 只能坐在 $2$ 号座位上．接下来若 $P_3$ 选择 $1$ 号座位时，$P_4$、$P_5$ 只能对号入座（这种坐法已经列出）；若 $P_3$ 选择 $4$ 号座位时，$P_4$ 能选择 $5$ 号 或 $1$ 号座位，而 $P_5$ 只能坐剩下的那个座位（其中一种已经列出）；若 $P_3$ 选择 $5$ 号座位时，$P_4$ 只能坐 $4$ 号座位，$P_5$ 只能坐 $1$ 号座位． -
若乘客 $P_1$ 坐到了 $2$ 号座位，其他乘客按规则就座，求乘客 $P_5$ 坐到 $5$ 号座位的概率．标注答案乘客 $P_5$ 坐到 $5$ 号座位的概率为 $\dfrac12$解析写出所有可能的就座方法是解决本题的关键．若乘客 $P_1$ 坐到了 $2$ 号座位，其他乘客按规则就坐，则所有可能的坐法可用下表表示：
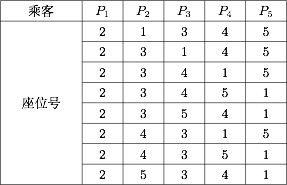于是，所有可能的坐法共 $8$ 种．设“乘客 $P_5$ 坐到 $5$ 号座位”为事件 $A$，则事件 $A$ 中的基本事件的个数为 $4$，由古典概型，得\[P\left(A\right)=\dfrac48=\dfrac12.\]答：乘客 $P_5$ 坐到 $5$ 号座位的概率为 $\dfrac12$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
