如图，椭圆 $E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$（$a>b>0$）的离心率是 $\dfrac{\sqrt2}{2}$，过点 $P \left( 0 , 1\right)$ 的动直线 $l$ 与椭圆相交于 $A$，$B$ 两点．当直线 $l$ 平行于 $x$ 轴时，直线 $l$ 被椭圆 $E$ 截得的线段长为 $2\sqrt2$．
【难度】
【出处】
无
【标注】
-
求椭圆 $E$ 的方程；标注答案椭圆 $E$ 的方程为 $\dfrac{x^2}{4}+\dfrac{y^2}{2}=1$．解析本题考查椭圆的基本量与方程，由已知条件列方程组，解出 $a$，$b$ 的值即可．由已知，可得点 $\left(\sqrt2,1\right)$ 在椭圆 $E$ 上，因此\[\begin{cases}
\dfrac{2}{a^2}+\dfrac{1}{b^2}=1,\\a^2-b^2\overset {\left[a\right]}=c^2,\\\dfrac ca\overset {\left[b\right]}=\dfrac{\sqrt2}{2}
.\end{cases}\]（推导中用到 $\left[a\right]$，$\left[b\right]$．）解得\[\begin{cases}a=2,\\b=\sqrt2.
\end{cases}\]所以椭圆 $E$ 的方程为 $\dfrac{x^2}{4}+\dfrac{y^2}{2}=1$． -
在平面直角坐标系 $xOy$ 中，是否存在与点 $P$ 不同的定点 $Q$，使得 $\dfrac{ \left|QA \right|}{ \left|QB \right|}=\dfrac{ \left|PA \right|}{ \left|PB \right|}$ 恒成立？若存在，求出点 $Q$ 的坐标；若不存在，请说明理由．标注答案存在与点 $P$ 不同的定点 $Q\left(0,2\right)$，使得 $\dfrac{ \left|QA \right|}{ \left|QB \right|}=\dfrac{ \left|PA \right|}{ \left|PB \right|}$ 恒成立．解析先由直线 $l$ 斜率为零时的特殊位置分析出可能存在的点在 $y$ 轴上，再由直线 $l$ 斜率不存在时求得满足条件的点为 $\left(0,2\right)$，最后利用点共线时的斜率相等证明该点适合于任意的直线 $l$ 即可．当直线 $l$ 与 $x$ 轴平行时，设直线 $l$ 与椭圆相交于 $C$，$D$ 两点．如果存在定点 $Q$ 满足条件，则有\[\dfrac{ \left|QC \right|}{ \left|QD \right|}=\dfrac{ \left|PC \right|}{ \left|PD \right|}=1,\]即 $ \left|QC \right|= \left|QD \right|$．所以点 $Q$ 在 $y$ 轴上，可设点 $Q$ 的坐标为 $\left(0,y_0\right)$．
当直线 $l$ 与 $x$ 轴垂直时，设直线 $l$ 与椭圆相交于 $M$，$N$ 两点，则 $M$，$N$ 的坐标分别为 $\left(0,\sqrt2\right)$，$\left(0,-\sqrt2\right)$．
由 $\dfrac{ \left|QM \right|}{ \left|QN \right|}=\dfrac{ \left|PM \right|}{ \left|PN \right|}$，得\[\dfrac{ \left|y_0-\sqrt2 \right|}{ \left|y_0+\sqrt2 \right|}=\dfrac{\sqrt2-1}{\sqrt2+1},\]解得\[y_0=1 或 y_0=2 .\]所以若存在不同于点 $P$ 的定点 $Q$ 满足条件，则点 $Q$ 的坐标只可能为 $\left(0,2\right)$．
下面证明：对任意直线 $l$，均有 $\dfrac{ \left|QA \right|}{ \left|QB \right|}=\dfrac{ \left|PA \right|}{ \left|PB \right|}$．
当直线 $l$ 的斜率不存在时，由上可知，结论成立．
当直线 $l$ 的斜率存在时，可设直线 $l$ 的方程为 $y=kx+1$，点 $A$，$B$ 的坐标分别为 $\left(x_1,y_1\right)$，$\left(x_2,y_2\right)$．
联立$\begin{cases}
\dfrac{x^2}{4}+\dfrac{y^2}{2}=1,\\y=kx+1,
\end{cases}$ 得\[\left(2k^2+1\right)x^2+4kx-2=0.\]其判别式 $\Delta =\left(4k\right)^2+8\left(2k^2+1\right)>0$，由韦达定理，得\[x_1+x_2=-\dfrac{4k}{2k^2+1} , x_1x_2=-\dfrac{2}{2k^2+1} .\]因此\[\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{x_1+x_2}{x_1x_2}=2k.\]易知，点 $B$ 关于 $y$ 轴对称的点 $B'$ 的坐标为 $\left(-x_2,y_2\right)$．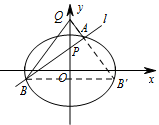
又\[k_{QA}=\dfrac{y_1-2}{x_1}=k-\dfrac{1}{x_1} , \\ k_{QB'}=\dfrac{y_2-2}{-x_2}=-k+\dfrac1{x_2}=k-\dfrac1{x_1},\]所以 $k_{QA}=k_{QB'}$，即 $Q$，$A$，$B'$ 三点共线，所以\[\dfrac{ \left|QA \right|}{ \left|QB \right|}=\dfrac{ \left|QA \right|}{ \left|QB' \right|}=\dfrac{ \left|x_1 \right|}{ \left|x_2 \right|}=\dfrac{ \left|PA \right|}{ \left|PB \right|} .\]故存在与点 $P$ 不同的定点 $Q\left(0,2\right)$，使得 $\dfrac{ \left|QA \right|}{ \left|QB \right|}=\dfrac{ \left|PA \right|}{ \left|PB \right|}$ 恒成立．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
