如图，三棱锥 $P-ABC$ 中，$PA\perp 平面ABC$，$PA=1$，$AB=1$，$AC=2$，$\angle BAC=60^\circ$．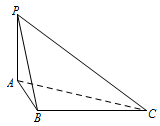
【难度】
【出处】
无
【标注】
-
求三棱锥 $P-ABC$ 的体积；标注答案三棱锥 $P-ABC$ 的体积为 $\dfrac{\sqrt3}{6}$．解析本题属于三棱锥求体积问题，底面积和高均容易确定，难度不大．由题设 $AB=1$，$AC=2$，$\angle BAC=60^\circ$，可得\[S_{\triangle ABC}\overset {\left[a\right]}=\dfrac12\cdot AB\cdot AC\cdot \sin{60^\circ}=\dfrac{\sqrt3}{2}.\]（推导中用到 $\left[a\right]$．）
由 $PA\perp 平面ABC$，可知 $PA$ 是三棱锥 $P-ABC$ 的高．又 $PA=1$，所以三棱锥 $P-ABC$ 的体积\[V\overset {\left[b\right]}=\dfrac13\cdot S_{\triangle ABC}\cdot PA=\dfrac{\sqrt3}{6}.\]（推导中用到 $\left[b\right]$．） -
证明：在线段 $PC$ 上存在点 $M$，使得 $AC\perp BM$，并求 $\dfrac{PM}{MC}$ 的值．标注答案证明略，$\dfrac{PM}{MC}= \dfrac13$．解析本题是线面垂直的判定和性质的综合应用，过 $B$ 点作出 $AC$ 的垂面是关键．如图，在平面 $ABC$ 内，过点 $B$ 作 $BN\perp AC$，垂足为 $N$．在平面 $PAC$ 内，过点 $N$ 作 $MN\parallel PA$ 交 $PC$ 于点 $M$，连接 $BM$．
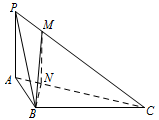由 $PA\perp 平面ABC$，知 $PA\perp AC$，所以 $MN\perp AC$．
由于 $BN \cap MN=N$，故 $AC\perp 平面MBN$．
又 $BM\subset 平面MBN$，所以 $AC\perp BM$．
在 ${\mathrm {Rt}} { \triangle BAN}$ 中，\[AN=AB\cdot \cos{\angle BAC}=\dfrac12,\]从而 $NC=AC-AN=\dfrac32$．由 $MN\parallel PA$，得\[\dfrac{PM}{MC}=\dfrac{AN}{NC}=\dfrac13.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
