在如图所示的多面体中，四边形 $AB{B_1}{A_1}$ 和 $AC{C_1}{A_1}$ 都为矩形．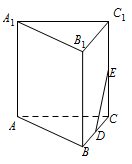
【难度】
【出处】
2014年高考四川卷（文）
【标注】
-
若 $AC \perp BC$，证明：直线 $BC \perp 平面 AC{C_1}{A_1}$；标注答案略．解析根据线面垂直的判定定理证明即可．因为四边形 $AB{B_1}{A_1}$ 和 $AC{C_1}{A_1}$ 都是矩形，所以 $A{A_1} \perp AB$，$A{A_1} \perp AC$．因为 $ AB$，$AC $ 为平面 $ ABC $ 内的两条相交直线，所以 $A{A_1} \perp 平面 ABC $．因为直线 $BC \subset 平面 ABC $，所以 $A{A_1} \perp BC$．又由已知，$AC \perp BC$，$A{A_1}\cap AC=A$，所以 $BC \perp 平面 AC{C_1}{A_1}$．
-
设 $D$，$E$ 分别是线段 $BC$，$C{C_1}$ 的中点，在线段 $AB$ 上是否存在一点 $M$，使直线 $DE\parallel 平面 {A_1}MC$？请证明你的结论．标注答案线段 $ AB $ 上存在一点 $ M $（线段 $ AB $ 的中点），使得直线 $DE \parallel 平面{A_1}MC$．解析由 $D$，$E$ 分别是线段 $BC$，$C{C_1}$ 的中点，易猜想 $ M $ 应为 线段 $ AB $ 的中点，接下来证明猜想成立即可．取线段 $ AB $ 的中点 $ M $，连接 ${A_1}M$，$MC$，$ MD$，${A_1}C$，$A{C_1}$，设 ${A_1}C\cap A{C_1}=O$．并连接 $ OM $，$OE $．
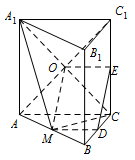因为四边形 $AC{C_1}{A_1}$ 为矩形，所以 $ O $ 为 $A{C_1}$ 的中点，则 $ MD$，$OE $ 分别为 $\triangle ABC$，$\triangle AC{C_1}$ 的中位线．
所以 $MD \parallel AC$，$OE \parallel AC$，$MD = \dfrac{1}{2}AC$，$OE = \dfrac{1}{2}AC$．
所以 $ MD \parallel OE$，$MD = OE$．
从而四边形 $ MDEO $ 为平行四边形，则 $DE\parallel MO$．
因为直线 $DE \not\subset 平面 {A_1}MC$，$MO \subset 平面 {A_1}MC$，
所以直线 $DE \parallel 平面 {A_1}MC$．
即线段 $ AB $ 上存在一点 $ M $（线段 $ AB $ 的中点），使得直线 $DE \parallel 平面{A_1}MC$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
