某高校共有学生 $ 15000 $ 人,其中男生 $ 10500 $ 人,女生 $ 4500 $ 人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集 $ 300 $ 位学生每周平均体育运动时间的样本数据(单位:小时).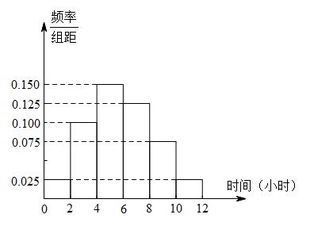

【难度】
【出处】
2014年高考安徽卷(文)
【标注】
-
应收集多少位女生的样本数据?标注答案应该收集 $90 $ 位女生的样本数据.解析由分层抽样的概念不难求解.因为 $\dfrac{300}{15000} \times 4500 = 90$.所以,应该收集 $90 $ 位女生的样本数据.
-
根据这 $ 300 $ 个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为:$\left[0,2\right] $,$ \left(2, 4\right] $,$ \left(4 , 6\right] $,$ \left(6 , 8\right] $,$ \left(8 , 10\right] $,$\left(10 , 12\right]$.估计该校学生每周平均体育运动时间超过 $ 4 $ 个小时的概率.标注答案该校学生每周平均体育运动时间超过 $4 $ 小时的概率的估计值为 $0.75 $.解析先用频率估计概率,再用样本估计总体.由频率分布直方图,得\[P\left(X > 4\right) = 2\left(0.15 + 0.125 + 0.075 + 0.025\right) = 0.75.\]所以该校学生每周平均体育运动时间超过 $4 $ 小时的概率的估计值为 $0.75 $.
-
在样本数据中,有 $ 60 $ 位女生的每周平均体育运动时间超过 $ 4 $ 个小时.请完成每周平均体育运动时间与性别的列联表,并判断是否有 $95\% $ 的把握认为“该校学生的每周平均体育运动时间与性别有关”.\[\begin{array}{|c|c|c|c|c|} \hline
P\left( {K^2} \geqslant {k_0}\right) & 0.10 & 0.05 & 0.010 & 0.005 \\ \hline
{k_0} & 2.706 & 3.841 & 6.635 & 7.879 \\ \hline \end{array}\]附:${K^2} = \dfrac{{n{{\left(ad - bc\right)}^2}}}{\left(a + b\right)\left(c + d\right)\left(a + c\right)\left(b + d\right)}$.标注答案每周平均运动时间与性别列联表如下:\[\begin{array}{|c|c|c|c|} \hline & 运动超过4小时 & 运动不超过4小时 & 合计 \\ \hline 男生 & 165 & 45 & 210 \\ \hline 女生 & 60 & 30 & 90 \\ \hline 合计 & 225 & 75 & 300 \\ \hline \end{array}\]有 $95\% $ 的把握认为“该校学生的每周平均体育运动时间与性别有关”.解析本题考查独立性检验.每周平均运动时间与性别列联表如下:\[\begin{array}{|c|c|c|c|} \hline & 运动超过4小时 & 运动不超过4小时 & 合计 \\ \hline 男生 & 165 & 45 & 210 \\ \hline 女生 & 60 & 30 & 90 \\ \hline 合计 & 225 & 75 & 300 \\ \hline \end{array} \\ \begin{split}{K^2} & = \dfrac{{n{{\left(ad - bc\right)}^2}}}{\left(a + b\right)\left(c + d\right)\left(a + c\right)\left(b + d\right)} \\& = \dfrac{{300{{\left(165 \cdot 30 - 60 \cdot 45\right)}^2}}}{225 \cdot 75 \cdot 210 \cdot 90} \\& \approx 4.762 > 3.841,\end{split}\]所以,有 $95\% $ 的把握认为“该校学生的每周平均体育运动时间与性别有关”.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3