如图，四棱锥 $P - ABCD$ 的底面是边长为 $ 8 $ 的正方形，四条侧棱长均为 $2\sqrt {17} $．点 $G$，$E$，$F$，$H$ 分别是棱 $PB$，$AB$，$CD$，$PC$ 上共面的四点，平面 $GEFH \perp 平面 ABCD$，$BC\parallel 平面 GEFH$．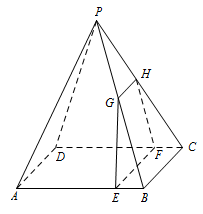
【难度】
【出处】
2014年高考安徽卷（文）
【标注】
-
证明：$GH\parallel EF$；标注答案略．解析根据线面平行的性质来证明．因为 $ BC\parallel 平面 GEFH$，$BC \subset 平面PBC$，$平面PBC \cap 平面GEFH=GH$．
所以 $GH\parallel BC$；同理可证 $EF\parallel BC$．所以 $ GH\parallel EF$． -
若 $EB = 2$，求四边形 $GEFH$ 的面积．标注答案四边形 $ GEFH $ 的面积为 $ 18 $．解析本题考查截面分析，易知四边形 $ GEFH $ 为梯型，接下来要求相关线段的长，这也是难点．连接 $AC $、$BD $，交点记为点 $O$，设 $ BD $ 交 $ EF $ 于点 $ N $，连接 $ OP $，$ GN $．
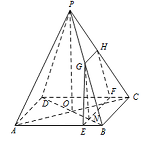因为 $ PA = PB = PC = PD = 2\sqrt {17} $，$O$ 为对角线的交点，所以 $ PO \perp AC$，$PO \perp BD$，$ AC \cap BD=O $，所以 $ PO \perp 平面 ABCD$．
因为 平面 $GEFH \perp 平面 ABCD$，且 $PO \not\subset 平面 GEFH $，所以 $PO\parallel 平面 GEFH$．
又 $ 平面PBD\cap 平面GEFH=GN$，所以 $PO\parallel GN$且 $ GN\perp 底面ABCD $，所以 $ GN $ 是梯形 $ GEFH $ 的高．因为 $ AB=8 $，$ EB=2 $，所以 $\dfrac{EB}{AB} =\dfrac{NB}{DB}=\dfrac14$，所以\[NB=\dfrac14DB=\dfrac{1}{2}OB,\]即 $ N $ 为 $ OB $ 中点．又因为 $ PO\parallel GN $，所以 $GN=\dfrac12PO $，即 $ G $ 为 $ PB $ 中点，且 $GH=\dfrac12BC=4 $，由已知可得\[OB=4\sqrt2,PO=\sqrt{{PB}^2-{OB}^2}=\sqrt{68-32}=6 ,\]所以 $GN=3$，故四边形 $ GEFH $ 的面积\[S=\dfrac12\left(GH+EF\right)GN=18. \]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
