如图,已知两条抛物线 ${E_1}:{y^2} = 2{p_1}x\left({p_1} > 0\right)$ 和 ${E_2}:{y^2} = 2{p_2}x\left({p_2} > 0\right)$,过原点 $O$ 的两条直线 ${l_1}$ 和 ${l_2}$,${l_1}$ 与 ${E_1}$,${E_2}$ 分别交于 ${A_1}$,${A_2}$ 两点,${l_2}$ 与 ${E_1}$,${E_2}$ 分别交于 ${B_1}$,${B_2}$ 两点.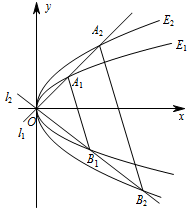

【难度】
【出处】
无
【标注】
-
证明:${A_1}{B_1}\parallel {A_2}{B_2}$;标注答案略.解析写出向量 $\overrightarrow{A_1 B_1}$ 和 $\overrightarrow{A_2 B_2} $,通过证明向量的平行来证明结论.设直线 $ l_1$,$l_2 $ 的方程分别为 $ y=k_1x$,$y=k_2x $ $ \left(k_1,k_2\ne0\right)$.
联立方程$\begin{cases}
y = {k_1}x, \\
{y^2} = 2{p_1}x, \\
\end{cases}$ 得 ${A_1} \left( \dfrac{{2{p_1}}}{k_1^2},\dfrac{{2{p_1}}}{k_1} \right) $.
联立 $ \begin{cases}y=k_1x,\\y^2=2{p_2}x,\end{cases}$ 得 ${A_2} \left( \dfrac{{2{p_2}}}{k_1^2},\dfrac{{2{p_2}}}{k_1} \right) $.
同理可得\[ {B_1} \left( \dfrac{{2{p_1}}}{k_2^2},\dfrac{{2{p_1}}}{k_2} \right) , {B_2} \left( \dfrac{{2{p_2}}}{k_2^2},\dfrac{{2{p_2}}}{k_2} \right) .\]所以\[\overrightarrow{A_1 B_1}\overset {\left[a\right]}=2{p_1}\left(\dfrac{1}{k_2^2}-\dfrac{1}{k_1^2},\dfrac{1}{k_2}-\dfrac{1}{k_1}\right),\\ \overrightarrow{A_2 B_2}=2{p_2}\left(\dfrac{1}{k_2^2}-\dfrac{1}{k_1^2},\dfrac{1}{k_2}-\dfrac{1}{k_1}\right). \](推导中用到 $\left[a\right]$.)故 $\overrightarrow{A_1 B_1}=\dfrac{p_1}{p_2}\overrightarrow{A_2 B_2} $,所以 ${A_1}{B_1}\parallel {A_2}{B_2}$. -
过原点 $O$ 作直线 $l$(异于 ${l_1},{l_2}$)与 ${E_1}$,${E_2}$ 分别交于 ${C_1}$,${C_2}$ 两点.记 $\triangle {A_1}{B_1}{C_1}$ 与 $\triangle {A_2}{B_2}{C_2}$ 的面积分别为 ${S_1}$ 与 ${S_2}$,求 $\dfrac{S_1}{S_2}$ 的值.标注答案$ \dfrac{S_1}{S_2}= \dfrac{p_1^2}{p_2^2} $.解析利用第一题的结论,可得三角形相似,进而可以根据共线比例值得出面积比.由(1)知:${A_1}{B_1}\parallel {A_2}{B_2}$.同理可知,${A_1}{C_1}\parallel {A_2}{C_2}$,$ {B_1}{C_1}\parallel {B_2}{C_2}$,所以\[\triangle {A_1}{B_1}{C_1} \backsim \triangle {A_2}{B_2}{C_2},\]所以\[ \dfrac{S_1}{S_2} \overset {\left[a\right]}= {\left(\dfrac{\left|\overrightarrow{A_1B_1}\right|}{\left|\overrightarrow{A_2B_2}\right|}\right)^2}= \dfrac{p_1^2}{p_2^2}.\](推导中用到 $\left[a\right] $.)
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2