如图，在三棱柱 $ABC - {A_1}{B_1}{C_1}$ 中，侧棱 $A{A_1} \perp 底面 ABC$，$AB = AC = 2A{A_1} = 2$，$\angle BAC = {120^ \circ }$，$D$，${D_1}$ 分别是线段 $BC$，${B_1}{C_1}$ 的中点，点 $P$ 是线段 $AD$ 上异于端点的点．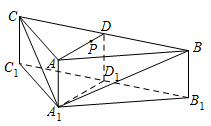
【难度】
【出处】
2013年高考四川卷（文）
【标注】
-
在平面 $ABC$ 内，试作出过点 $P$ 与平面 ${A_1}BC$ 平行的直线 $l$，请说明理由，并证明直线 $l \perp 平面 AD{D_1}{A_1}$；标注答案在平面 $ABC$ 内，过点 $P$ 作直线 $l\parallel BC$，如图所示：
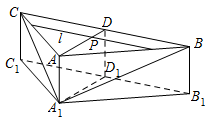理由和证明略解析根据线面平行的判定定理可作出直线 $l$，再由线面垂直的判定定理来证明．在平面 $ABC$ 内，过点 $P$ 作直线 $l\parallel BC$，如图， 因为 $l$ 在平面 ${A_1}BC$ 外，$BC$ 在平面 ${A_1}BC$ 内，
由直线与平面平行的判定定理可知，$l\parallel 平面 {A_1}BC$．
由已知，$AB = AC$，点 $D$ 是 $BC$ 的中点，所以 $BC \perp AD$，则直线 $l \perp AD$．
因为 $A{A_1} \perp 平面 ABC$，所以 $A{A_1} \perp l$．
又因为 $AD$，$A{A_1}$ 在平面 $AD{D_1}{A_1}$ 内，且 $AD$ 与 $A{A_1}$ 相交，所以直线 $l \perp 平面 AD{D_1}{A_1}$． -
设（1）中的直线 $l$ 交 $AC$ 于点 $Q$，求三棱锥 ${A_1} - Q{C_1}D$ 的体积．
（锥体体积公式：$V = \dfrac{1}{3}Sh$，其中 $S$ 为底面面积，$h$ 为高）标注答案三棱锥 ${A_1} - Q{C_1}D$ 的体积是 $\dfrac{\sqrt 3 }{6}$解析选择 $ \triangle A_1QC_1 $ 为棱锥的底面计算体积简单．过点 $D$ 作 $DE \perp AC$ 于 $E$．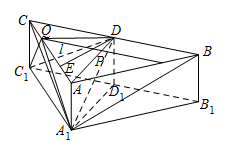
因为 $A{A_1} \perp 平面 ABC$，所以 $A{A_1} \perp DE$．
又因为 $AC$，$A{A_1}$ 在平面 $A{A_1}{C_1}C$ 内，且 $AC$ 与 $A{A_1}$ 相交，所以 $DE \perp 平面 A{A_1}{C_1}C$．由\[AB = AC = 2,\angle BAC = 120^\circ,\]有\[AD = 1,\angle DAC = 60^\circ.\]在 $\triangle ADE$ 中，\[DE = \dfrac{\sqrt 3 }{2}AD = \dfrac{\sqrt 3 }{2},\]又\[{S_{\triangle {A_1}Q{C_1}}} = \dfrac{1}{2}{A_1}{C_1} \cdot A{A_1} = 1,\]所以\[\begin{split}{V_{{A_1} - Q{C_1}D}} &\overset {\left[a\right]}= {V_{D-{A_1}Q{C_1}}}\\ &= \dfrac{1}{3}DE \cdot {S_{\triangle {A_1}Q{C_1}}} \\&= \dfrac{1}{3} \cdot \dfrac{\sqrt 3 }{2} \cdot 1 \\&= \dfrac{\sqrt 3 }{6}.\end{split}\]（推导中用到 $\left[a\right]$．）因此三棱锥 ${A_1} - Q{C_1}D$ 的体积是 $\dfrac{\sqrt 3 }{6}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
