如图，四棱锥 $P - ABCD$ 的底面 $ABCD$ 是边长为 $ 2 $ 的菱形，$\angle BAD = {60^ \circ }$．已知 $PB = PD = 2$，$PA = \sqrt 6 $．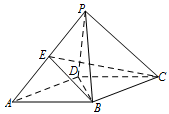
【难度】
【出处】
2013年高考安徽卷（文）
【标注】
-
证明：$PC \perp BD$；标注答案略解析利用线面垂直证明线线垂直．连接 $ AC $，交于 $ BD $ 于 $O$ 点，连接 $ PO $．
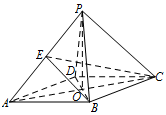因为底面 $ ABCD $ 是菱形，所以 $AC \perp BD$，$BO = DO$．
由 $PB = PD$ 知，$PO \perp BD$．
又因为 $PO \cap AC = O$，所以 $BD \perp 面 APC$，因此 $BD \perp PC $． -
若 $E$ 为 $PA$ 的中点，求三棱锥 $P - BCE$ 的体积．标注答案三棱锥 $P - BCE$ 的体积为 $ \dfrac{1}{2} $解析本题考查三棱锥体积的求法．因为 $ E $ 是 $ PA $ 的中点，所以\[\begin{split}{V_{P - BCE}}& \overset {\left[a\right]}= {V_{C - PEB}}\\& = \dfrac{1}{2}{V_{C - PAB}} \\&= \dfrac{1}{2}{V_{B - APC}}.\end{split}\]（推导中用到 $\left[a\right] $．）由 $PB = PD = AB = AD = 2$ 知，$\triangle ABD \cong \triangle PBD$．因为 $\angle BAD = {60^ \circ }$，所以\[PO = AO = \sqrt 3 ,AC = 2\sqrt 3 ,BO = 1.\]又\[PA = \sqrt 6 ,P{O^2} + A{O^2} = P{A^2},\]即 $ PO \perp AC $，故\[{S_{\triangle APC}} = \dfrac{1}{2}PO \cdot AC = 3.\]由（1）知，$BO \perp 面APC$，因此\[\begin{split}{V_{P - BCE}} &\overset {\left[b\right]}= \dfrac{1}{2}{V_{B - APC}} \\&= \dfrac{1}{2} \cdot \dfrac{1}{3} \cdot BO \cdot {S_{\triangle APC}} \\&= \dfrac{1}{2} . \end{split}\]（推导中用到 $\left[b\right] $．）
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
