小波以游戏方式决定是去打球、唱歌还是去下棋,游戏规则为:以 $O$ 为起点,再从 ${A_1}$,${A_2}$,${A_3}$,${A_4}$,${A_5}$,${A_6}$(如图所示)这 $ 6 $ 个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为 $X$,若 $X > 0$ 就去打球,若 $X = 0$ 就去唱歌,若 $X < 0$ 就去下棋.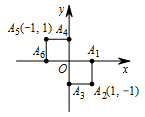
【难度】
【出处】
2013年高考江西卷(文)
【标注】
-
写出数量积 $X$ 的所有可能取值;标注答案$X$ 的所有可能取值为 $ - 2$,$ - 1$,$0$,$1 $解析本题考查平面向量的数量积.数量积$X$ 的所有可能取值为 $ - 2$,$ - 1$,$0$,$1 $.
-
分别求小波去下棋的概率和不去唱歌的概率.标注答案小波去下棋的概率为 $ \dfrac{7}{15}$,不去唱歌的概率为 $\dfrac{11}{15}$解析本题考查古典概型,涉及平面向量数量积的运算,属中档题.数量积为 $ - 2$ 的有 $\overrightarrow {O{A_2}} \cdot \overrightarrow {O{A_5}}$,共 $ 1 $ 种;
数量积为 $ - 1$ 的有\[\overrightarrow {O{A_1}} \cdot \overrightarrow {O{A_5}} ,\overrightarrow {O{A_1}} \cdot \overrightarrow {O{A_6}} ,\overrightarrow {O{A_2}} \cdot \overrightarrow {O{A_4}} ,\overrightarrow {O{A_2}} \cdot \overrightarrow {O{A_6}} ,\overrightarrow {O{A_3}} \cdot \overrightarrow {O{A_4}} ,\overrightarrow {O{A_3}} \cdot \overrightarrow {O{A_5}} ,\]共 $ 6 $ 种;
数量积为 $ 0 $ 的有\[\overrightarrow {O{A_1}} \cdot \overrightarrow {O{A_3}} ,\overrightarrow {O{A_1}} \cdot \overrightarrow {O{A_4}} ,\overrightarrow {O{A_3}} \cdot \overrightarrow {O{A_6}} ,\overrightarrow {O{A_4}} \cdot \overrightarrow {O{A_6}} ,\]共 $ 4 $ 种;
数量积为 $ 1 $ 的有\[\overrightarrow {O{A_1}} \cdot \overrightarrow {O{A_2}},\overrightarrow {O{A_2}} \cdot \overrightarrow {O{A_3}} ,\overrightarrow {O{A_4}} \cdot \overrightarrow {O{A_5}} ,\overrightarrow {O{A_5}} \cdot \overrightarrow {O{A_6}} ,\]共 $ 4 $ 种.
故所有可能的情况共有 $ 15 $ 种.
所以小波去下棋的概率为 ${p_1} = \dfrac{7}{15}$.因为去唱歌的概率为 ${p_2} = \dfrac{4}{15}$,所以小波不去唱歌的概率为\[p \overset {\left[a\right]}= 1 - {p_2} = \dfrac{11}{15}.\](推导中用到 $\left[a\right]$.)
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2