如图，直四棱柱 $ABCD - {A_1}{B_1}{C_1}{D_1}$ 中，$AB\parallel CD$，$AD \perp AB$，$AB = 2$，$AD = \sqrt 2$，$A{A_1} = 3$，$E$ 为 $CD$ 上一点，$DE = 1$，$EC = 3$．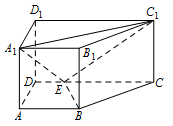
【难度】
【出处】
2013年高考江西卷（文）
【标注】
-
证明：$BE \perp 平面B{B_1}{C_1}C$；标注答案略解析由线面垂直的判定定理知，需要在面内找两条相交直线与已知直线垂直．其中利用直棱柱的性质容易证出 $BB_1 \perp BE$，而 $BC \perp BE $ 可以利用勾股定理逆定理证出．如图，过点 $B$ 作 $CD$ 的垂线交 $CD$ 于点 $F$．
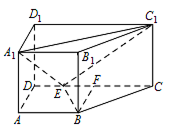则\[\begin{split}BF &= AD = \sqrt 2 ,\\ EF &= AB - DE = 1,\\ FC &= 2.\end{split}\]在 ${\mathrm{Rt}} \triangle BFE$ 中，$BE = \sqrt 3 $．
在 ${\mathrm{Rt}} \triangle CFB$ 中，$BC = \sqrt 6 $．
在 $\triangle BEC$ 中，因为\[B{E^2} + B{C^2} = 9 = E{C^2},\]故 $BE \perp BC$．
由 $B{B_1} \perp 平面 ABCD$，得 $BE \perp B{B_1}$，而 $B{B_1} \cap BC=B $，所以 $BE \perp 平面 B{B_1}{C_1}C$． -
求点 ${B_1}$ 到平面 $E{A_1}{C_1}$ 的距离．标注答案点 ${B_1}$ 到平面 $E{A_1}{C_1}$ 的距离为 $ \dfrac{{\sqrt {10} }}{5}$解析通过变换三棱锥的底面，利用等体积法即可求解．如图，连接 ${B_1}E$．
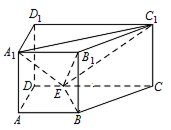则三棱锥 $E - {A_1}{B_1}{C_1}$ 的体积为\[V = \dfrac{1}{3}A{A_1} \cdot {S_{\triangle {A_1}{B_1}{C_1}}} = \sqrt 2 . \]在 ${\mathrm{Rt}} \triangle {A_1}{D_1}{C_1}$ 中，\[\begin{split} {A_1}{C_1} &= \sqrt {{A_1}D_1^2 + {D_1}C_1^2} \\ & = 3\sqrt 2 ,\end{split} \]同理，\[\begin{split} E{C_1} &= \sqrt {E{C^2} + CC_1^2} \\ & = 3\sqrt 2, \\ {A_1}E &= \sqrt {{A_1}{A^2} + A{D^2} + D{E^2}} \\ & = 2\sqrt 3 ,\end{split} \]故\[{S_{\triangle {A_1}{C_1}E}} = 3\sqrt 5.\]设点 ${B_1}$ 到平面 $E{A_1}{C_1}$ 的距离为 $d$，则三棱锥 ${B_1} - E{A_1}{C_1}$ 的体积\[\begin{split} V = \dfrac{1}{3} \cdot d \cdot {S_{\triangle E{A_1}{C_1}}} = \sqrt 5 d,\end{split} \]从而 $\sqrt 5 d = \sqrt 2$，\[d = \dfrac{{\sqrt {10} }}{5}.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
