如图,某公司要在 $A,B$ 两地连线上的定点 $C$ 处建造广告牌 $CD $,其中 $D$ 为顶端,$AC$ 长 $35$ 米,$CB$ 长 $80$ 米.设点 $A,B$ 在同一水平面上,从 $A$ 和 $B$ 看 $D$ 的仰角分别为 $\alpha $ 和 $\beta $.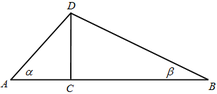

【难度】
【出处】
2014年高考上海卷(文)
【标注】
-
设计中 $CD$ 是铅垂方向.若要求 $\alpha \geqslant 2\beta $,问 $CD$ 的长至多为多少(结果精确到 $0.01$ 米)?标注答案至多为 $28.28$ 米解析设出 $CD$ 的长,表达出 $\tan \alpha$ 和 $\tan \beta$,由 $\tan \alpha \geqslant \tan {2\beta}$ 可解.设 $CD = h$,由题意得\[\tan \alpha \geqslant \tan 2\beta > 0,\]又\[\tan \alpha = \dfrac{h}{35},\tan \beta = \dfrac{h}{80},\]所以\[\dfrac{h}{35} \geqslant \dfrac{{2 \times \dfrac{h}{80}}}{{1 - {{\left( {\dfrac{h}{80}} \right)}^2}}} > 0,\]解得\[h \leqslant 20\sqrt 2 \approx 28.28,\]所以,$CD$ 的长至多约为 $ 28.28 $ 米.
-
施工完成后,$CD$ 与铅垂方向有偏差.现在实测得 $\alpha = 38.12^\circ , \beta = 18.45^\circ $,求 $CD$ 的长(参考数据:$\sin\alpha=0.617,\cos\alpha=0.787,\sin\beta=0.316,\cos\beta=0.787,\sin\left(\alpha+\beta\right)=0.835,\sin\left(\alpha-\beta\right)=0.949$,结果精确到 $0.01$ 米)标注答案$26.93$ 米解析由正弦定理在 $\triangle ABD$ 中可求出 $BD$,再在 $\triangle BCD$ 中由余弦定理可求出 $CD$.在 $\triangle ABD$ 中,$\alpha + \beta = {56.57^ \circ },AB = 115$,由正弦定理得\[\dfrac{BD}{\sin \alpha } = \dfrac{AB}{{\sin \left( {\alpha + \beta } \right)}},\]解得\[BD \approx 58.064.\]在 $\triangle BCD$ 中,由余弦定理得\[C{D^2} = B{C^2} + B{D^2} - 2BC \cdot BD\cos \beta,\]解得\[CD \approx 26.93.\]所以,$CD$ 的长约是 $26.93$ 米.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2