${y^2} = 4x $．

本题是对抛物线定义的考查，根据抛物线的定义可以简化焦半径的计算．设 $Q\left( {{x_0},4} \right)$，代入 ${y^2} = 2px$，得 ${x_0} = \dfrac{8}{p}$，所以\[ | {PQ} | = \dfrac{8}{p}.\]根据抛物线定义可得\[\left| {QF} \right| = \dfrac{p}{2} + {x_0} = \dfrac{p}{2} + \dfrac{8}{p}.\]由题设得\[\dfrac{p}{2} + \dfrac{8}{p} = \dfrac{5}{4} \times \dfrac{8}{p},\]解得\[p = - 2 \left(舍去\right) 或 p = 2,\]所以 $ C $ 的方程为 ${y^2} = 4x $．

\[x - y - 1 = 0 或 x + y - 1 = 0.\]

关键条件是“四点共圆”，由此 $AB$ 的垂直平分线 $MN$ 为圆的直径，圆心为 $MN$ 的中点，因此有 $|AE|=|BE|=\dfrac{1}{2}|MN|$ 的等量关系，进而联立直线与抛物线，表示线段的长度，求得方程．由题设知 $l$ 与坐标轴不垂直，故可设 $l$ 的方程为 $x = my + 1\left( {m \ne 0} \right)$，代入 ${y^2} = 4x$得\[{y^2} - 4my - 4 = 0.\]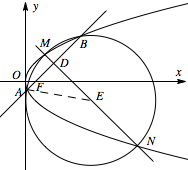设 $A\left( {{x_1},{y_1}} \right)$，$B\left({{x_2},{y_2}} \right)$，则\[\begin{split}{y_1} + {y_2} &= 4m, {y_1}{y_2} &= - 4.\end{split}\]故 $AB$ 的中点为 $D\left( {2{m^2} + 1,2m} \right)$，弦 $AB$ 的长度为\[ \left| {AB} \right| = \sqrt {{m^2} + 1} \left| {{y_1} - {y_2}} \right| = 4\left( {{m^2} + 1} \right). \]又 $l'$ 的斜率为 $ - m$，所以 $ l'$ 的方程为\[x = - \dfrac{1}{m}y + 2{m^2} + 3.\]将上式代入 ${y^2} = 4x$，并整理得\[{y^2} + \dfrac{4}{m}y - 4\left( {2{m^2} + 3} \right) = 0.\]设 $M\left( {{x_3},{y_3}} \right)$，$N\left( {{x_4},{y_4}} \right),$ 则\[ {y_3} + {y_4} = - \dfrac{4}{m}, {y_3}{y_4} = - 4\left( {2{m^2} + 3} \right). \]故 $MN$ 的中点为 $E\left( {\dfrac{2}{m^2} + 2{m^2} + 3, - \dfrac{2}{m}} \right)$，弦 $MN$ 的长度为\[ \left| {MN} \right| = \sqrt {1 + \dfrac{1}{m^2}} \left| {{y_3} - {y_4}} \right| = \dfrac{{4\left( {{m^2} + 1} \right)\sqrt {2{m^2} + 1} }}{m^2}. \]由于 $MN$ 垂直平分线 $AB$，故 $A,M,B,N$ 四点在同一圆上等价于\[\left| {AE} \right| = \left| {BE} \right| = \dfrac{1}{2}\left| {MN} \right|.\]则根据直线与圆的位置关系有\[\dfrac{1}{4}{\left| {AB} \right|^2} + {\left| {DE} \right|^2} = \dfrac{1}{4}{\left| {MN} \right|^2},\]即\[4{\left( {{m^2} + 1} \right)^2} + {\left( {2m + \dfrac{2}{m}} \right)^2} + {\left( {\dfrac{2}{m^2} + 2} \right)^2} = \dfrac{{4{{\left( {{m^2} + 1} \right)}^2}\left( {2{m^2} + 1} \right)}}{m^4},\]化简得 ${m^2} - 1 = 0$，解得\[m = 1 或 m = - 1,\]所求直线 $l$ 的方程为\[x - y - 1 = 0 或 x + y - 1 = 0.\]