双曲线 $x^2-\dfrac{y^2}{b^2}=1\left(b>0\right)$ 的左、右焦点分别为 $F_1,F_2$，直线 $l$ 过 $F_2$ 且与双曲线交于 $A,B$ 两点．
【难度】
【出处】
无
【标注】
-
若 $l$ 的倾斜角为 $\dfrac{\mathrm {\mathrm \pi} }2$，$\triangle F_1AB$ 是等边三角形，求双曲线的渐近线方程；标注答案$ y=\pm \sqrt{2}x $解析小题考查双曲线的对称性．根据题意，通径 $ |AB|=2b^2 $ 与焦距 $ |F_1F_2|=2c $ 的比为 $ 2:\sqrt 3 $，即 $ \dfrac{b^2}{c}=\dfrac{2}{\sqrt 3} $，从而解得 $ b^2=2 $，进而双曲线的渐近线方程为 $ y=\pm \sqrt{2}x $．
-
设 $b=\sqrt 3$，若 $l$ 的斜率存在，且 $\left(\overrightarrow{F_1A}+\overrightarrow{F_1B}\right)\cdot \overrightarrow{AB}=0$，求 $l$ 的斜率．标注答案$\pm \dfrac{\sqrt{15} }{5} $解析本小问利用向量描述了一个弦的中点问题，用“有心二次曲线的垂径定理”即可轻松解决．此时双曲线方程为 $ x^2-\dfrac{y^2}3=1 $，$ F_1\left(-2,0\right) $，$ F_2\left(2,0\right) $．如图，由题意，$ A,B $ 两点分别位于双曲线的两支上，且 $ \left|AF_1\right|=\left|BF_1\right| $，设线段 $ AB $ 的中点为 $ M $．
方法一
该双曲线的左准线为 $ l_1:x=-\dfrac{1}{2} $，由于 $ A,B $ 两点分别位于左准线 $ l_1 $ 的左右两边，且到 $ l_1 $ 的距离相等，故点 $ M $ 落在 $ l_1 $ 上．
设点 $M$ 坐标为 $\left(-\dfrac{1}{2},m\right) $，则\[\overrightarrow{F_1M}\cdot\overrightarrow{F_2M}=\left(\dfrac{3}{2},m \right)\cdot\left(-\dfrac{5}{2},m \right)=m^2-\dfrac{15}{4}= 0, \]解得 $m=\pm \dfrac{\sqrt{15} }{2}$，所以直线 $l$ 的斜率为 $\pm \dfrac{\sqrt{15} }{5} $．
方法二
设 $M\left(n,m\right)$，$A\left(x_1,y_1\right)$，$B\left(x_2,y_2\right)$，直线 $l$ 的斜率为 $k$．将 $A,B$ 两点满足的双曲线方程相减整理（即双曲线的“垂径定理”）可得 $\dfrac mn\cdot k=3$．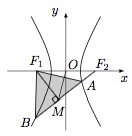
因此有\[\begin{cases} \dfrac mn\cdot k=3,\\ \dfrac{m}{n+2}\cdot k=-1,\\ \dfrac{m}{n-2}=k,\end{cases}\]解得 $n=-\dfrac 12$，从而 $m=-\dfrac{3}{2k}=-\dfrac{5k}2$，进而 $k=\pm \dfrac{\sqrt{15}}5$，所以直线 $l$ 的斜率为 $\pm \dfrac{\sqrt{15} }{5} $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
