如图，四棱锥 $P-ABCD$ 中，$PA\perp 底面 ABCD$，$AD\parallel BC$，$AB=AD=AC=3$，$PA=BC=4$，$M$ 为线段 $AD$ 上一点，$AM=2MD$，$N$ 为 $PC$ 的中点．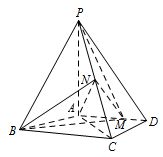
【难度】
【出处】
2016年高考全国丙卷（文）
【标注】
-
证明 $MN\parallel 平面 PAB$；标注答案略解析线面平行可利用线线平行来进行证明，本题就是构造平行四边形证明线线平行，进而得到线面平行．由已知得 $AM=\dfrac 23 AD=2$，
如图，取 $BP$ 中点 $T$，连接 $AT,TN$，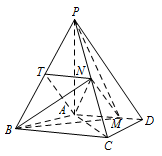
由 $N$ 为 $PC$ 的中点知 $TN\parallel BC$，且 $TN=\dfrac 12 BC=2$，
又 $AD\parallel BC$，故 $TN\parallel AM$，且 $TN=AM$，
所以四边形 $AMNT$ 为平行四边形，
所以 $MN\parallel AT$，
因为 $AT\subset 平面 PAB$，$MN \not\subset 平面 PAB$，
所以 $MN\parallel 平面 PAB$． -
求四面体 $N-BCM$ 的体积．标注答案$ \dfrac {4\sqrt 5}3 $解析本题关键是求 $\triangle {BCM}$ 的面积，以 $BC$ 为底，点 $M$ 到 $BC$ 的距离转化为点 $A$ 到 $BC$ 的距离．因为 $PA\perp 面 ABCD$，$N$ 为 $PC$ 的中点，所以 $N$ 到平面 $ABCD$ 的距离为 $\dfrac 12PA$．
取 $BC$ 的中点 $E$，连接 $AE$．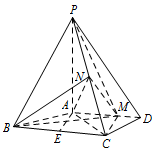
由 $AB=AC=3$ 得\[AE\perp BC,AE=\sqrt {AB^2-BE^2}=\sqrt 5.\]由 $AM\parallel BC$ 得 $M$ 到 $BC$ 的距离为 $\sqrt 5$，故\[S_{\triangle BCM}=\dfrac 12\times 4\times \sqrt 5=2\sqrt 5.\]所以四面体 $N-BCM$ 的体积\[V_{N-BCM}=\dfrac 13S_{\triangle BCM}\times \dfrac {PA}2=\dfrac {4\sqrt 5}3.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
