已知抛物线 $C:y^2=2x$ 的焦点为 $F$，平行于 $x$ 轴的两条直线 $l_1,l_2$ 分别交 $C$ 于 $A,B$ 两点，交 $C$ 的准线于 $P,Q$ 两点．
【难度】
【出处】
无
【标注】
-
若 $F$ 在线段 $AB$ 上，$R$ 是 $PQ$ 的中点，证明 $AR\parallel FQ$；标注答案略解析本题可以通过抛物线的光学性质直接证明．连接 $PF,RF$，如图：
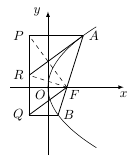由抛物线的光学性质知 $AP=AF$，$BQ=BF$，从而有\[\angle AFP+\angle QFB=\dfrac 12\left({\mathrm \pi} -\angle PAF\right)+\dfrac 12\left({\mathrm \pi} -\angle QBF\right)=\dfrac {\mathrm \pi} {2},\]所以 $PF\perp FQ$，又\[RF=\dfrac 12PQ=PR=QR,\]从而可得 $\triangle PAR$ 与 $\triangle FAR$ 全等，所以 $PF\perp AR$，从而有 $AR\parallel FQ$． -
若 $\triangle{PQF}$ 的面积是 $\triangle{ABF}$ 的面积的两倍，求 $AB$ 中点的轨迹方程．标注答案$ y^2=x-1 $解析本题涉及到坐标系中三角形的面积计算，合理选择参数即可．设点 $A\left(2a^2,2a\right)$，$B\left(2b^2,2b\right)$，则 $P\left(-\dfrac 12,2a\right)$，$Q\left(-\dfrac 12,2b\right)$，且 $AB$ 的中点$M\left(a^2+b^2,a+b\right)$．
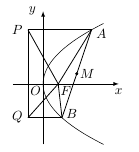由 $\triangle PQF$ 的面积是 $\triangle ABF$ 的面积的两倍可得\[\dfrac 12\cdot |2a-2b|\cdot \left[\dfrac 12-\left(-\dfrac 12\right)\right]=2\cdot \dfrac 12\left|\left(2a^2-\dfrac 12\right)\cdot 2b-\left(2b^2-\dfrac 12\right)\cdot 2a\right|,\]化简得 $|4ab+1|=1$，解得 $ab=-\dfrac 12$（舍去 $ab=0$）．进而消参可得 $M$ 的轨迹方程为 $y^2=x-1$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
