$ f'\left(x\right)=-2a\sin{2x}+\left(1-a\right)\sin x$

本题考查基本的导数运算．函数 $f\left(x\right)$ 的导函数\[f'\left(x\right)=-2a\sin{2x}+\left(1-a\right)\sin x.\]

$ A=\begin{cases} 2-3a,& a\in\left(0,\dfrac 15\right),\\ \dfrac 18\left(a+\dfrac{1}{a}+6\right),&a\in \left[\dfrac 15,1\right],\\3a-2,&a\in \left(1,+\infty\right).\end{cases} $

本题考查对含参二次函数的讨论．由二倍角公式，整理得\[f\left(x\right)=2a\cos ^2x+\left(a-1\right)\cos x-1,\]令 $t=\cos x$（$t\in \left[-1,1\right]$），有\[g\left(t\right)=2at^2+\left(a-1\right)t-1,t\in \left[-1,1\right],\]则函数 $|f\left(x\right)|$ 的最大值 $A$ 即函数 $|g\left(t\right)|$ 的最大值．按二次函数 $g\left(t\right)$ 的对称轴 $t=\dfrac{1-a}{4a}$ 是否在区间 $\left[-1,1\right]$ 内展开讨论．
情形一：当 $\dfrac{1-a}{4a}\in \left[-1,1\right]$ 即 $a\in\left[\dfrac 15,+\infty\right)$ 时，函数 $|g\left(t\right)|$ 的最大值为\[\max\left\{\big|g\left(-1\right)\big|,\big|g\left(1\right)\big|,\left|g\left(\dfrac{1-a}{4a}\right)\right|\right\}.\]情形二：当 $\dfrac{1-a}{4a}\not\in \left[-1,1\right]$ 即 $a\in\left(0,\dfrac 15\right)$ 时，函数 $|g\left(t\right)|$ 的最大值为\[\max\left\{\big|g\left(-1\right)\big|,\big|g\left(1\right)\big|\right\}.\]事实上，有\[\big|g\left(-1\right)\big|=a,\big|g\left(1\right)\big|=|3a-2|,\left|g\left(\dfrac{1-a}{4a}\right)\right|=\dfrac 18\left(a+\dfrac{1}{a}+6\right).\]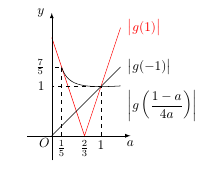注意到当 $a=\dfrac 15$ 和 $a=1$ 时三者的取值，结合作差比较大小，可得\[A=\begin{cases} 2-3a,& a\in\left(0,\dfrac 15\right),\\ \dfrac 18\left(a+\dfrac{1}{a}+6\right),&a\in \left[\dfrac 15,1\right],\\3a-2,&a\in \left(1,+\infty\right).\end{cases}\]

略

本小题是第（1）（2）小题的简单综合，适当放缩不难解决．由第（1）小题知\[f'\left(x\right)=-2a\sin{2x}+\left(1-a\right)\sin x.\]当 $a\in\left(0,\dfrac 15\right)$ 时，有\[|f'\left(x\right)|\leqslant |2a|+|1-a|=1+a\leqslant 4-6a=2A.\]当 $a\in \left[\dfrac 15,1\right]$ 时，有 $|f'\left(x\right)|\leqslant 1+a$，而 $2A=\dfrac 14\left(a+\dfrac{1}{a}+6\right)$，由分析法，可得\[|f'\left(x\right)|\leqslant 2A\Leftarrow \left(3a+1\right)\left(a-1\right)\leqslant 0,\]这显然成立．
当 $a\in \left(1,+\infty\right)$ 时，有\[|f'\left(x\right)|\leqslant |2a|+|a-1|=3a-1\leqslant 6a-4=2A.\]综上知，$|f'\left(x\right)|\leqslant 2A$．