如图，已知正三棱锥 $P-ABC$ 的侧面是直角三角形，$PA=6$．顶点 $P$ 在平面 $ABC$ 内的正投影为点 $D$，$D$ 在平面 $PAB$ 内的正投影为点 $E$，连接 $PE$ 并延长交 $AB$ 于点 $G$．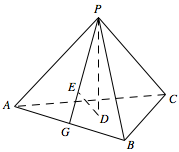
【难度】
【出处】
2016年高考全国乙卷（文）
【标注】
-
证明：$G$ 是 $AB$ 的中点；标注答案略解析本题主要考查点在面内的正投影的概念以及线面垂直的判定．因为 $P$ 在平面 $ABC$ 内的正投影为 $D$，
所以 $PD\perp 平面 ABC$，
所以 $PD\perp AB$．
同理，因为 $D$ 在平面 $PAB$ 内的正投影为 $E$，
所以 $DE\perp 平面 PAB$，
所以 $DE\perp AB$．
因为 $PD\cap DE=D$，
所以 $AB\perp 平面 PDE$，
所以 $AB\perp PG$．
又因为 $PA=PB$，
所以 $G$ 为 $AB$ 中点． -
在答题卡第（18）题的图中作出点 $E$ 在平面 $PAC$ 内的正投影 $F$（说明作法及理由），并求四面体 $PDEF$ 的体积．标注答案$V=\dfrac43$解析选择合适的底面是求三棱锥的体积的关键．作法如下：
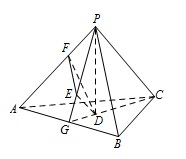在平面 $PAB$ 内，过点 $E$ 作 $EF\parallel PB$，交 $PA$ 于点 $F$，则 $F$ 即为点 $E$ 在平面 $PAC$ 内的正投影．
证明：因为 $PA\perp PB$，$PC\perp PB$，$PA\cap PC=P$，
所以 $PB\perp 平面 PAC$．
因为 $EF\parallel PB$，
所以 $EF\perp 平面 PAC$，
故点 $F$ 为点 $E$ 在平面 $PAC$ 内的正投影．
因为 $DE\perp 平面 PAB$，
故 $DE$ 为点 $D$ 到平面 $PFE$ 的距离，且 $DE=2$（$D$ 为底面中心，故 $DE=\dfrac13PC$），
同时可知 $E$ 为 $\triangle PAB$ 的重心，所以 $F$ 是 $PA$ 的三等分点，因此 $PF=2$，$EF=2$．
又 $S_{\triangle{PFE}}=\dfrac 12\cdot PF\cdot EF=\dfrac 12\cdot 2\cdot 2=2$，
所以 $V_{D-PFE}=\dfrac 13 \cdot DE\cdot S_{\triangle{PFE}}=\dfrac 13\cdot 2\cdot 2=\dfrac 43$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
