某公司计划购买 $1$ 台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个 $200$ 元.在机器使用期间,如果备件不足再购买,则每个 $500$ 元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了 $100$ 台这种机器在三年使用期内更换的易损零件数,得下面柱状图: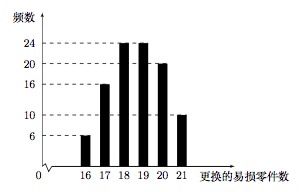 记 $x$ 表示 $1$ 台机器在三年使用期内需要换的易损零件数,$y$ 表示 $1$ 台机器在购买易损零件上所需的费用(单位:元),$n$ 表示购机的同时购买的易损零件数.
记 $x$ 表示 $1$ 台机器在三年使用期内需要换的易损零件数,$y$ 表示 $1$ 台机器在购买易损零件上所需的费用(单位:元),$n$ 表示购机的同时购买的易损零件数.
 记 $x$ 表示 $1$ 台机器在三年使用期内需要换的易损零件数,$y$ 表示 $1$ 台机器在购买易损零件上所需的费用(单位:元),$n$ 表示购机的同时购买的易损零件数.
记 $x$ 表示 $1$ 台机器在三年使用期内需要换的易损零件数,$y$ 表示 $1$ 台机器在购买易损零件上所需的费用(单位:元),$n$ 表示购机的同时购买的易损零件数.【难度】
【出处】
2016年高考全国乙卷(文)
【标注】
-
若 $n=19$,求 $y$ 与 $x$ 的函数解析式;标注答案$y$ 与 $x$ 的函数关系式为 $y=\begin{cases}3800,&x\leqslant 19\\ 500x-5700,&x>19\end{cases},x\in\mathbb N$解析根据题中条件分段表示出 $x$,$y$ 的关系即可.若 $n=19$,当一台机器三年内使用的易损零件数 $x\leqslant 19$ 时,$y=19\times 200=3800\left( 元 \right)$;
当一台机器三年内使用的易损零件数 $x>19$ 时,$y=19\times 200+\left(x-19\right)\times 500=500x-5700\left( 元 \right)$.
综上,$y$ 与 $x$ 的函数关系式为 $y=\begin{cases}3800,&x\leqslant 19\\ 500x-5700,&x>19\end{cases},x\in\mathbb N$ -
若要求“需更换的易损零件数不大于 $n$”的频率不小于 $0.5$,求 $n$ 的最小值;标注答案$19$解析从频率分布直方图中找到频率为 $0.5$ 的易损零件数在哪一组是解决本题的核心.$n$ 表示购买 $1$ 台机器的同时购买的易损零件数,则若使 $P\left(X\leqslant n\right)\geqslant 0.5$,则 $n$ 的最小值为 $19$.因为\[\begin{split}&P\left(X\leqslant 18\right)=0.06+0.16+0.24=0.46<0.5,\\&P\left(X\leqslant 19\right)=0.46+0.24=0.7\geqslant 0.5.\end{split}\]
-
假设这 $100$ 台机器在购机的同时每台都购买 $19$ 个易损零件,或每台都购买 $20$ 个易损零件,分别计算这 $100$ 台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买 $1$ 台机器的同时应购买 $19$ 个还是 $20$ 个易损零件?标注答案购买一台机器同时购买 $19$ 个易损零件解析分别计算出两种情况的费用进行比较即可.每台都购买 $19$ 个易损零件所用的总费用设为 $y_{1}$,则\[y_{1}=19\times 200\times 100+500\times 20+500\times 2\times 10=400000,\]每台都购买 $20$ 个易损零件所用的总费用设为 $y_{2}$,则\[y_{2}=20\times 200\times 100+ 500\times 10=405000.\]所以购买 $19$ 件易损零件所需要用的平均数为 $4000$,购买 $20$ 件易损零件所需要用的平均数为 $4050$,故因为 $4000<4050$,所以购买一台机器同时购买 $19$ 个易损零件.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3