如图，$\triangle OAB$ 是等腰三角形，$\angle AOB=120^\circ$，以 $O$ 为圆心，$\dfrac 12 OA$ 为半径作圆．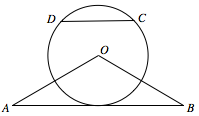
【难度】
【出处】
无
【标注】
-
证明：直线 $AB$ 与 $\odot O$ 相切；标注答案略解析本题考查直线与圆相切的证明，可根据圆心与切点的连线垂直于该直线，并且圆心到直线距离等于半径来证明．作 $AB$ 的中点 $E$，连接 $OE$，则 $OE\perp AB$．
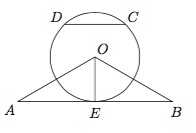在等腰三角形 $OAB$ 中，$\angle AOB=120^{\circ}$，所以 $\angle OAB=30^{\circ}$，故\[OE=OA\sin \angle OAB=\dfrac{1}{2}OA.\]综上 $AB$ 与圆 $O$ 相切． -
点 $C,D$ 在 $\odot O$ 上，且 $A,B,C,D$ 四点共圆，证明：$AB\parallel CD$．标注答案略解析根据四点共圆设出圆心位置，并根据题中条件得出圆心满足的特点是解决本题的关键．设 $A,B,C,D$ 四点共圆的圆心为 $O'$，$CD$ 的中点为 $F$，
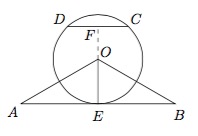则 $O'E\perp AB$，$O'F\perp CD$，又 $OE\perp AB$，$OF\perp CD$，
所以 $O,O',E$ 三点共线，$O,O',F$ 三点共线，
故 $O,O',E,F$ 四点共线，即 $OO'\perp AB$，$OO'\perp CD$，所以 $AB\parallel CD$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
