设圆 $x^2+y^2+2x-15=0$ 的圆心为 $A$，直线 $l$ 过点 $B\left(1,0\right)$ 且与 $x$ 轴不重合，$l$ 交圆 $A$ 于 $C,D$ 两点，过 $B$ 作 $AC$ 的平行线交 $AD$ 于点 $E$．
【难度】
【出处】
无
【标注】
-
证明：$|EA|+|EB|$ 为定值，并写出点 $E$ 的轨迹方程；标注答案$|EA|+|EB|=4$，轨迹方程为 $\dfrac{x^2}{4}+\dfrac{y^2}3=1\left(y\neq 0\right)$．解析本小题利用几何知识证明 $|EB|=|ED|$ 即可；将圆的方程化为标准方程\[\left(x+1\right)^2+y^2=16.\]
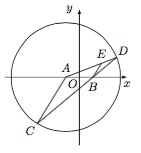由于 $BE\parallel AC$，于是 $\angle EBD=\angle ACD$．又 $|AC|=|AD|$，于是 $\angle ACD=\angle ADC$，因此 $\angle EBD=\angle EDB$，从而 $|EB|=|ED|$，这样就得到了\[|EA|+|EB|=|EA|+|ED|=|AD|\]为定值 $4$．根据椭圆的定义，点 $E$ 的轨迹方程为\[\dfrac{x^2}{4}+\dfrac{y^2}3=1\left(y\neq 0\right).\] -
设点 $E$ 的轨迹为曲线 $C_1$，直线 $l$ 交 $C_1$ 于 $M,N$ 两点，过 $B$ 且与 $l$ 垂直的直线与圆 $A$ 交于 $P,Q$ 两点，求四边形 $MPNQ$ 面积的取值范围．标注答案四边形 $MPNQ$ 的面积的取值范围是 $\left[12,8\sqrt 3\right)$．解析本小题是典型的面积问题，计算两个弦长 $|MN|$ 和 $|PQ|$ 即可，其中对焦点弦长的计算用到了《高考数学压轴题的分析与解》中破解压轴题有效10招中的第3招，与之类似的题有2014年天津卷理科第19题．设 $\angle MBA=\theta$（$\theta \in \left(0,{\mathrm \pi} \right)$），则在 $\triangle MAB$ 中应用余弦定理，有\[|MA|^2=|MB|^2+|AB|^2-2\cdot |MB|\cdot |AB|\cdot\cos\theta,\]结合 $|MA|+|MB|=4$ 可解得\[|MB|=\dfrac{3}{2-\cos\theta}.\]
类似的，可得\[|NB|=\dfrac{3}{2+\cos\theta},\]从而\[|MN|=|MB|+|NB|=\dfrac{12}{4-\cos^2\theta}.\]此时直线 $PQ$ 的方程为\[x\cos\theta =y\sin\theta +\cos\theta,\]于是圆的弦长\[|PQ|=2\sqrt{4^2-\left(\dfrac{2\cos\theta}{\sqrt{\cos^2\theta+\sin^2\theta}}\right)^2}=4\sqrt{4-\cos^2\theta}.\]于是可得四边形 $MPNQ$ 的面积\[S=\dfrac 12\cdot |MN|\cdot |PQ|=\dfrac{24}{\sqrt{4-\cos^2\theta}},\]于是四边形 $MPNQ$ 的面积的取值范围是 $\left[12,8\sqrt 3\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
