如图,菱形 $ABCD$ 的对角线 $AC$ 与 $BD$ 交于点 $O$,点 $E,F$ 分别在 $AD,CD$ 上,$AE=CF$,$EF$ 交 $BD$ 于点 $H$.将 $\triangle DEF$ 沿 $EF$ 折到 $\triangle D'EF$ 的位置.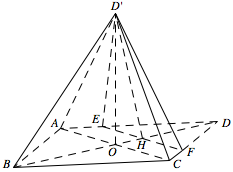

【难度】
【出处】
2016年高考全国甲卷(文)
【标注】
-
证明:$AC\perp HD'$;标注答案略解析可以通过线面垂直来证线线垂直.因为 $DA=DC$,$AE=CF$,所以 $\dfrac{DE}{DA}=\dfrac{DF}{DC}$,所以 $AC\parallel EF$.
在菱形 $ABCD$ 中,$AC\perp BD$,所以 $DH\perp EF$,$OH\perp EF$,
即 $D'H\perp EF$,$OH\perp EF$,又 $D'H\cap OH=H$,
所以 $EF\perp $ 平面 $D'HO$,
所以 $AC\perp $ 平面 $D'HO$,故 $AC\perp HD'$. -
若 $AB=5$,$AC=6$,$AE=\dfrac 54$,$OD'=2\sqrt 2$,求五棱锥 $D'-ABCFE$ 的体积.标注答案$\dfrac {23\sqrt 2}2$解析要求五棱锥 $D'-ABCFE$ 的体积,关键是计算底面面积和高.因为 $AE= \dfrac{5}{4}$,$AD=5$,由第 $(1)$ 问可知 $EF\parallel AC$,所以 $\dfrac{DH}{OH}=\dfrac{DE}{AE}=\dfrac{3}{1}$.
在菱形 $ABCD$ 中,由 $AB=5$,$AC=6$,可得 $OD=4$.所以 $OH=1$,$HD'=3$.
在 $\triangle D'OH$ 中,\[D'H^{2}=OH^{2}+D'O^{2},\]所以 $\triangle D'OH$ 为直角三角形,且 $D'O\perp OH$,又由第 $(1)$ 问可知 $AC\perp $ 平面 $D'HO$,所以 $AC\perp D'O$.又 $AC\cap OH=O$,所以 $D'O\perp $ 平面 $ABCD$.
底面五边形的面积为\[\begin{split}S_{五边形ABCFE}&=S_{四边形ABCD}-S_{\triangle DEF}\\&=\dfrac{1}{2}\times 6\times 8-\dfrac {1}{2}\times \dfrac 92\times 3\\&=\dfrac {69}4.\end{split}\]所以五棱锥的体积\[\begin{split}V_{D'-ABCFE}&=\dfrac{1}{3}\cdot S_{五边形ABCFE}\cdot D'O\\&=\dfrac{1}{3}\times \dfrac {69}4\times 2\sqrt 2\\&=\dfrac {23\sqrt 2}2.\end{split}\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2