如图，菱形 $ABCD$ 的对角线 $AC$ 与 $BD$ 交于点 $O,AB=5,AC=6$，点 $E,F$ 分别在 $AD,CD$ 上，$AE=CF=\dfrac 54,EF$ 交 $BD$ 于点 $H$．将 $\triangle DEF$ 沿 $EF$ 折到 $\triangle D'EF$ 的位置，$OD'=\sqrt {10}$．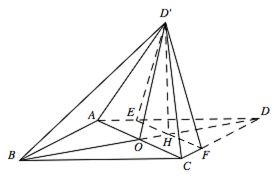
【难度】
【出处】
无
【标注】
-
证明：$D'H\perp 平面 ABCD$；标注答案略解析要证明 $D'H\perp 平面 ABCD$，只需在平面 $ABCD$ 内找到两条相交直线，使 $D'H$ 与这两条直线都垂直即可．易发现直线 $EF$ 满足，关键是找另一条，可由勾股定理的逆定理来寻找．因为 $AE=CF=\dfrac{5}{4}$，所以 $\dfrac{AE}{AD}=\dfrac{CF}{CD}$，$EF\parallel AC$．
因为四边形 $ABCD$ 为菱形，所以 $AC\perp BD$，$EF\perp BD$，$EF\perp DH$，$EF\perp {D}'H$．
又因为 $AC=6$，所以 $AO=3$；
又 $AB=5$，$AO\perp OB$，所以 $OB=4$，$OH=\dfrac{AE}{AD}\cdot OD=1$，
所以 $DH={D}'H=3$，${{\left| O{D}' \right|}^{2}}={{\left| OH \right|}^{2}}+{{\left| D'H \right|}^{2}}$，$D'H\perp OH$．
又因为 $OH\cap EF=H$，所以 $D'H\perp $ 面 $ABCD$． -
求二面角 $B-D'A-C$ 的正弦值．标注答案$\dfrac{2\sqrt{95}}{25}$解析建立空间直角坐标系，用向量法来解．如此思维难度较小．建立如图坐标系 $H-xyz$．
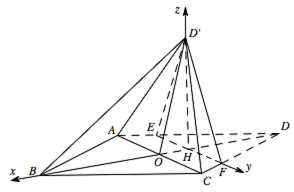则 $B\left( 5 , 0 , 0 \right)$，$C\left( 1 , 3 , 0 \right)$，$D'\left( 0 , 0 , 3 \right)$，$A\left( 1 , -3 , 0 \right)$；
同时 $\overrightarrow{AB}=\left( 4 , 3 , 0 \right)$，$\overrightarrow{AD'}=\left( -1 , 3 , 3 \right)$，$\overrightarrow{AC}=\left( 0 , 6 , 0 \right)$．
设面 $ABD'$ 的法向量$\overrightarrow{{{n}_{1}}}=\left( x , y , z \right)$，由\[\begin{cases}
\overrightarrow{{{n}_{1}}}\cdot \overrightarrow{AB}=0, \\
\overrightarrow{{{n}_{1}}}\cdot \overrightarrow{A{D}'}=0, \\
\end{cases} 即 \begin{cases}4x+3y=0, \\
-x+3y+3z=0 ,\\
\end{cases} \]取 $x=3$，则 $y=-4,z=5$，所以 $\overrightarrow{{{n}_{1}}}=\left( 3 , -4 , 5 \right)$．
同理可得面 $AD'C$ 的法向量 $\overrightarrow{{{n}_{2}}}=\left( 3 , 0 , 1 \right)$，所以\[\left| \cos \left\langle\overrightarrow{{{n}_{1}}},\overrightarrow{{{n}_{2}}} \right\rangle \right|=\dfrac{\left| \overrightarrow{{{n}_{1}}}\cdot \overrightarrow{{{n}_{2}}} \right|}{\left| \overrightarrow{{{n}_{1}}} \right|\left| \overrightarrow{{{n}_{2}}} \right|}=\dfrac{\left| 9+5 \right|}{5\sqrt{2}\cdot \sqrt{10}}=\dfrac{7\sqrt{5}}{25},\]因此所求二面角的正弦值为 $\dfrac{2\sqrt{95}}{25}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
