已知椭圆 $C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ 过 $A\left( 2,0 \right)$，$B\left( 0,1 \right)$ 两点．
【难度】
【出处】
无
【标注】
-
求椭圆 $C$ 的方程及离心率；标注答案$\dfrac{x^2}4+y^2=1$，$\dfrac{\sqrt 3}2$解析本题考查椭圆的方程与基本量．根据题意，有 $a=2$，$b=1$，于是椭圆的方程为\[\dfrac{x^2}4+y^2=1,\]其离心率 $e=\dfrac{\sqrt 3}2$．
-
设 $P$ 为第三象限内一点且在椭圆 $C$ 上，直线 $PA$ 与 $y$ 轴交于点 $M$，直线 $PB$ 与 $x$ 轴交于点 $N$，求证：四边形 $ABNM$ 的面积为定值．标注答案$2$解析本题考查基本的利用代数方法研究几何的能力，可以采用参数方程和仿射变换两种解法．法一：参数方程解法
设 $P$ 点坐标为 $\left(2\cos{\theta},\sin\theta\right)$，可求得 $M$ 点坐标为 $\left(0,\dfrac{\sin\theta}{1-\cos\theta}\right)$，$N$ 点坐标为 $\left(\dfrac{2\cos\theta}{1-\sin\theta},0\right)$，故\[\left|AN\right|\cdot\left|BM\right|=\left|\left(\dfrac{2\cos\theta}{1-\sin\theta}-2\right)\left(\dfrac{\sin\theta}{1-\cos\theta}-1\right)\right|=2\left|\dfrac{\left(\sin\theta+\cos\theta -1\right)^2}{\left(1-\sin\theta\right)\left(1-\cos\theta\right)}\right|=4.\]（推导中用到：）
所以四边形 $ABNM$ 的面积为 $\dfrac 12\cdot \left|AN\right|\cdot\left|BM\right|=2$．
法二：仿射变换解法
在仿射变换$\begin{cases} x'=x,\\ y'=2y\end{cases}$ 下椭圆 $C$ 变为圆 $C':x'^2+y'^2=4$．
设 $A,B,P,M,N$ 的对应点分别为 $A',B',P',M',N'$，如图．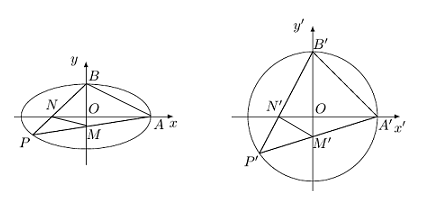
由 $\angle B'A'N'=\angle A'B'M'=45^\circ$，且\[\angle A'B'N'=45^\circ+\angle OB'N'=\angle P'+\angle OB'N'=\angle A'M'B',\]可得 $\triangle A'B'N'$ 与 $\triangle B'M'A'$ 相似，于是\[\dfrac{|A'N'|}{|B'A'|}=\dfrac{|A'B'|}{|B'M'|},{ 即 }|A'N'|\cdot |B'M'|=|A'B'|^2=8,\]因此\[|AN|\cdot 2|BM|=8,{ 即 }|AN|\cdot |BM|=4\]所以四边形 $ABNM$ 的面积为 $\dfrac 12\cdot \left|AN\right|\cdot\left|BM\right|=2$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
