如图，在四棱锥 $P-ABCD$ 中，$PA\perp CD$，$AD\parallel BC$，$\angle ADC=\angle PAB=90^\circ$，$BC=CD=\dfrac12AD$．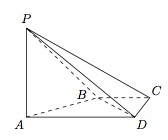
【难度】
【出处】
2016年高考四川卷（文）
【标注】
-
在平面 $PAD$ 内找一点 $M$，使得 $ 直线 CM\parallel 平面 PAB$，并说明理由；标注答案略解析本题的关键在于通过思考得出“点 $M$ 在平面 $PAD$ 和过 $C$ 且平行于平面 $PAB$ 的平面 的交线上”．如图，取棱 $AD$ 的中点 $M$（$M\in 平面 PAD$）．
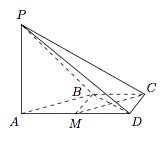点 $M$ 即为所求的一个点．理由如下：
因为 $AD\parallel BC$，$BC=\dfrac12AD$，所以 $BC\parallel AM$，且 $BC=AM$，所以四边形 $AMCB$ 是平行四边形，从而 $CM\parallel AB$．
又 $AB\subset 平面 PAB$，$CM\not\subset 平面 PAB$，所以 $CM\parallel 平面 PAB$．
（说明：取棱 $PD$ 的中点 $N$，则所找的点可以是直线 $MN$ 上任意一点） -
证明：$ 平面 PAB\perp 平面 PBD$．标注答案略解析证明面面垂直的方法为"在其中一个面上找到一条直线垂直于另一个平面"．由已知，$PA\perp AB$，$PA\perp CD$．
因为 $AD\parallel BC$，$BC=\dfrac12AD$，所以直线 $AB$ 与 $CD$ 相交，所以 $PA\perp 平面 ABCD$，从而 $PA\perp BD$．
因为 $AD\parallel BC$，$BC=\dfrac12AD$，所以 $BC\parallel MD$，且 $BC=MD$，所以四边形 $BCDM$ 是平行四边形．
所以 $BM=CD=\dfrac12AD$，所以 $BD\perp AB$，又 $AB\cap AP=A$，所以 $BD\perp 平面 PAB$．
又 $BD\subset 平面 PBD$，所以 $ 平面 PAB\perp 平面 PBD$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
