椭圆 $E$ 的方程为 $\dfrac{x^2}4+y^2=1$．

本小题考查椭圆的基本量与方程．根据题意，有 $a=2b$，结合点 $P\left(\sqrt 3,\dfrac 12\right)$ 在椭圆 $E$ 上，可得椭圆 $E$ 的方程为 $\dfrac{x^2}4+y^2=1$．

略

本小题是圆幂定理在仿射变换下的结果，因此可以考虑用仿射变换解决，同时利用参数方程计算也不难．需要注意的是这里出现了弦中点的问题，因此可以利用椭圆的“垂径定理”（参考《高考数学压轴题的分析与解》破解压轴题的有效10招中的第7招“有心二次曲线的「垂径定理」”）．设 $A\left(x_1,y_1\right)$，$B\left(x_2,y_2\right)$，将两个点满足的椭圆方程相减整理可得（即椭圆的“垂径定理”）直线 $OM$ 和直线 $AB$ 的斜率之积为 $-\dfrac 14$，从而直线 $CD$ 的斜率为 $-\dfrac 12$．
仿射变换解法：
注意到结论的形式类似于圆幂定理，因此考虑用仿射变换．作仿射变换 $x'=x$，$y'=2y$，则椭圆 $E$ 变为圆 $E':x'^2+y'^2=4$．设 $A,B,C,D$ 变化后的对应点分别是 $A',B',C',D'$，如图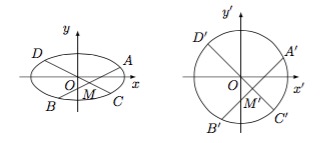． 根据仿射变换前后弦长的对应关系，我们有\[\dfrac{|M'A'|}{|MA|}=\dfrac{|M'B'|}{|MB|}=\dfrac{\sqrt{1+4\cdot\left(\dfrac 12\right)^2}}{\sqrt{1+\left(\dfrac 12\right)^2}},\]而\[\dfrac{|M'C'|}{|MC|}=\dfrac{|M'D'|}{|MD|}=\dfrac{\sqrt{1+4\cdot\left(-\dfrac 12\right)^2}}{\sqrt{1+\left(-\dfrac 12\right)^2}},\]于是可得\[\dfrac{|M'A'|}{|MA|}=\dfrac{|M'B'|}{|MB|}=\dfrac{|M'C'|}{|MC|}=\dfrac{|M'D'|}{|MD|},\]根据圆幂定理，有\[|M'A'|\cdot |M'B'|=|M'C'|\cdot |M'D'|,\]由此即得原命题成立．
参数方程解法：
由 $CD:y=-\dfrac 12x$，于是可设 $M\left(-2m,m\right)$，进而分别以 $\left(2,1\right)$ 和 $\left(2,-1\right)$ 为直线 $AB$ 和 $CD$ 的方向向量，可设\[AB:\begin{cases}x=-2m+2t,\\ y=m+t,\end{cases} 且 CD:\begin{cases} x=-2m+2t,\\ y=m-t.\end{cases} \]设点 $A,B$ 对应的参数分别为 $t_1,t_2$，点 $C,D$ 对应的参数分别为 $t_3,t_4$，分别将直线 $AB,CD$ 的方程与椭圆方程联立，可得 $t_1,t_2$ 是方程\[2t^2+2m^2-1=0\]的两根，而 $t_3,t_4$ 是方程\[2t^2-4mt+2m^2-1=0\]的两根．因此\[|MA|\cdot |MB|-|MC|\cdot |MD|= \sqrt{2^2+1}\cdot |t_1|\cdot \sqrt{2^2+1}\cdot |t_2|-\sqrt{2^2+\left(-1\right)^2}\cdot |t_3|\cdot \sqrt{2^2+\left(-1\right)^2}\cdot |t_4|=0,\]因此原命题得证．