已知椭圆 $E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$（$a>b>0$）的两个焦点与短轴的一个端点是直角三角形的三个顶点．直线 $l:y=-x+3$ 与椭圆 $E$ 有且只有一个公共点 $T$．
【难度】
【出处】
无
【标注】
-
求椭圆 $E$ 的方程及点 $T$ 的坐标；标注答案椭圆 $E$ 的方程为 $\dfrac{x^2}6+\dfrac{y^2}3=1$，$T\left(2,1\right)$．解析本小题综合考查椭圆的基本量与方程以及直线与圆锥曲线的位置关系．根据勾股定理，可得 $a^2+a^2=\left(2c\right)^2$，其中 $c$ 为椭圆的半焦距．又由直线 $l$ 与椭圆联立的等效判别式（直线 $Ax+By+C=0$ 与椭圆 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ 联立后的判别式与等效判别式 $\Delta_0=a^2A^2+b^2B^2-C^2$ 同号，这很容易利用联立方程证明．）可得\[a^2\cdot
1^2+b^2\cdot 1^2-\left(-3\right)^2=0,\]于是可得方程组\[\begin{cases} a^2=2c^2,\\a^2+b^2=9,\\
a^2=b^2+c^2,\end{cases} 解得 \begin{cases} a^2=6,\\ b^2=3,\\
c^2=3,\end{cases} \]于是椭圆 $E$ 的方程为 $\dfrac{x^2}6+\dfrac{y^2}3=1$，进而不难求出 $T\left(2,1\right)$． -
设 $O$ 是坐标原点，直线 $l'$ 平行于 $OT$，与椭圆 $E$ 交于不同的两点 $A,B$，且与直线 $l$ 交于点 $P$．证明：存在常数 $\lambda$，使得 $|PT|^2=\lambda |PA|\cdot |PB|$，并求 $\lambda$ 的值．标注答案存在 $\lambda=\dfrac45$ 使得 $|PT|^2=\dfrac45 |PA|\cdot |PB|$．解析本小题是圆幂定理在仿射变换下的结果，利用参数方程也可以很快计算出结果．仿射变换法：
注意到问题的结论类似于圆幂定理，因此考虑用仿射变换．作仿射变换 $x'=x$，$y'=\sqrt 2y$ 则椭圆 $E$ 变为圆\[E':x'^2+y'^2=6,\]此时设 $P,A,B,T$ 的对应点分别是 $P',A',B',T'$．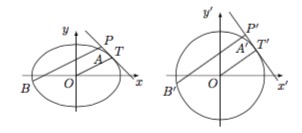
由仿射变换前后的弦长对应关系，可得\[\dfrac{|P'T'|^2}{|PT|^2}=\dfrac{1+2\cdot \left(-1\right)^2}{1+\left(-1\right)^2}=\dfrac
32,\]而\[\dfrac{|P'A'|\cdot |P'B'|}{|PA|\cdot
|PB|}=\dfrac{1+2\cdot\left(\dfrac 12\right)^2}{1+\left(\dfrac
12\right)^2}=\dfrac 65,\]两式相比，可得\[\dfrac{|PT|^2}{|PA|\cdot |PB|}\cdot \dfrac{|P'A'|\cdot
|P'B'|}{|P'T'|^2}=\dfrac 45,\]而根据圆幂定理，有\[|P'T'|^2=|P'A'|\cdot |P'B'|,\]因此原命题得证，且 $\lambda=\dfrac
45$．
参数方程解法：
设 $P$ 点坐标为 $\left(p,3-p\right)$，由题意，可设直线 $l'$ 的参数方程为\[\begin{cases}x=p+2t,\\y=3-p+t,\end{cases} \]其中 $t$ 为参数．将其与椭圆方程联立，得\[2t^2+4t+p^2-4p+4=0.\]设 $A,B$ 两点对应的参数分别为 $t_1,t_2$，则\[\begin{cases}\Delta>0,\\t_1+t_2=-2,\\t_1t_2=
\dfrac{\left(p-2\right)^2}{2}. \end{cases} \]因为\[|PT|^2=2\left(p-2\right)^2, |PA|\cdot|PB|=\sqrt{5}|t_1|\cdot\sqrt{5}|t_2|=\dfrac{5\left(p-2\right)^2}{2},\]所以存在常数 $\lambda=
\dfrac{4}{5} $，使得 $|PT|^2=\lambda |PA|\cdot |PB|$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
