某化肥厂生产甲、乙两种混合肥料，需要 $A,B,C$ 三种主要原料．生产 $1$ 车皮甲种肥料和生产 $1$ 车皮乙种肥料所需三种原料的吨数如下表所示：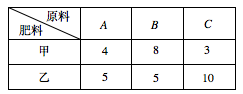
$$\begin{array}{|c|c|c|c|}\hline \text{肥料} \backslash \text{原料}&A&B&C \\ \hline \text{甲}&4&8&3 \\ \hline \text{乙}&5&5&10 \\ \hline \end{array}$$现有 $A$ 种原料 $200$ 吨，$B$ 种原料 $360$ 吨，$C$ 种原料 $300$ 吨，在此基础上生产甲、乙两种肥料．已知生产 $1$ 车皮甲种肥料，产生的利润为 $2$ 万元；生产 $1$ 车皮乙种肥料，产生的利润为 $3$ 万元．分别用 $x,y$ 表示计划生产甲、乙两种肥料的车皮数．
$$\begin{array}{|c|c|c|c|}\hline \text{肥料} \backslash \text{原料}&A&B&C \\ \hline \text{甲}&4&8&3 \\ \hline \text{乙}&5&5&10 \\ \hline \end{array}$$现有 $A$ 种原料 $200$ 吨，$B$ 种原料 $360$ 吨，$C$ 种原料 $300$ 吨，在此基础上生产甲、乙两种肥料．已知生产 $1$ 车皮甲种肥料，产生的利润为 $2$ 万元；生产 $1$ 车皮乙种肥料，产生的利润为 $3$ 万元．分别用 $x,y$ 表示计划生产甲、乙两种肥料的车皮数．【难度】
【出处】
2016年高考天津卷（文）
【标注】
-
用 $x,y$ 列出满足生产条件的数学关系式，并画出相应的平面区域；标注答案$x$，$y$ 满足的数学关系式为\[ \begin{cases}
4x+5y\leqslant 200 ,\\
8x+5y\leqslant 360, \\
3x+10y\leqslant 300, \\
x\geqslant 0, \\
y\geqslant 0. \\
\end{cases} \]该不等式组所表示的区域为图中的阴影部分．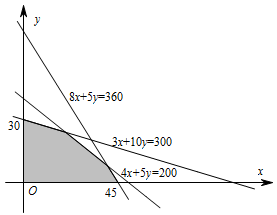
解析本题考查线性规划在实际生活中的应用，关键是分析实际条件列出不等式．然后按照线性规划的思想解决即可，注意 $x,y$ 均为正数．由已知，知 $x$，$y$ 满足的数学关系式为\[ \begin{cases}
4x+5y\leqslant 200 ,\\
8x+5y\leqslant 360, \\
3x+10y\leqslant 300, \\
x\geqslant 0, \\
y\geqslant 0. \\
\end{cases} \]该不等式组所表示的区域为图中的阴影部分． -
问分别生产甲、乙两种肥料各多少车皮，能够产生最大的利润？并求出此最大利润．标注答案生产甲种肥料 $20$ 车皮，乙种肥料 $24$ 车皮时利润最大，最大利润为 $112$ 万元解析本题在第一问可行域的前提下，分析目标函数的最值，得到最优解即可．设利润为 $z$ 万元，则目标函数 $z=2x+3y$，即 $y=-\dfrac {2}{3}x+\dfrac {z}{3}$．这是斜率为 $-\dfrac 23$，随 $z$ 变化的一族平行直线．
$\dfrac z3$ 为直线在 $y$ 轴上的截距，当 $\dfrac z3$ 取最大值时，$z$ 得最大值．根据 $(1)$ 知，如图．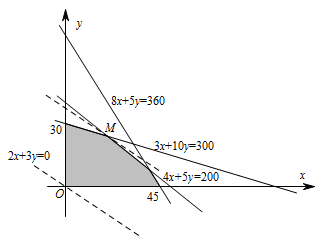
当直线 $z=2x+3y$ 经过平面区域中的点 $M$ 时，$z$ 取得最大值．解方程组\[ \begin{cases}4x+5y=200,\\ 3x+10y=300,\end{cases} \]得 $M\left(20,24\right)$，所以最大利润为 $2\times 20+3\times 24=112$ 万元．
答：生产甲种肥料 $20$ 车皮，乙种肥料 $24$ 车皮时利润最大，最大利润为 $112$ 万元．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
