如图，四边形 $ABCD$ 是平行四边形，$ 平面 AED\perp 平面 ABCD$，$EF\parallel AB$，$AB=2$，$BC=EF=1$，$AE=\sqrt 6$，$DE=3$，$\angle BAD=60^{\circ}$，$G$ 为 $BC$ 的中点．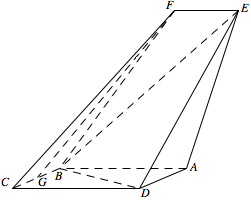
【难度】
【出处】
2016年高考天津卷（文）
【标注】
-
求证：$FG\parallel 平面 BED$；标注答案略解析证明线面平行，关键是找到平面内与线平行的直线．本题可以利用三角形的中位线，构造出平行四边形，从而找到面内直线．取 $BD$ 的中点为 $O$，连接 $OE$，$OG$．
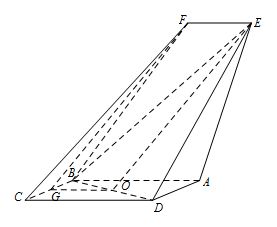在 $\triangle BCD$ 中，因为 $G$ 是 $BC$ 的中点，所以 $OG\parallel DC$ 且 $OG=\dfrac 12DC=1$．
又因为 $EF\parallel AB$，$AB\parallel DC$，
所以 $EF\parallel OG$ 且 $EF=OG $．
所以四边形 $OGFE$ 是平行四边形，所以 $GF\parallel OE$．
又因为 $GF\not \subset 平面 BED$，$OE \subset 平面 BED$，
所以 $GF\parallel 平面 BED$． -
求证：$ 平面 BED\perp 平面 AED$；标注答案略解析证明面面垂直的关键是：从其中的一个平面内找到另一个平面的垂线．分析条件可证 $BD \perp 平面 AED$．在 $\triangle ABD$ 中，$AD=1$，$AB=2$，$\angle BAD=60^\circ$．
由余弦定理可得 $BD=\sqrt 3$，进而可得 $\angle ADB=90^\circ$，即 $BD\perp AD$．
又因为平面 $AED\perp 平面 ABCD$，$BD \subset 平面 ABCD$，平面 $AED\cap 平面 ABCD=AD$，
所以 $BD \perp 平面 AED$．
又因为 $BD \subset 平面 BED$，
所以平面 $BED\perp 平面 AED$． -
求直线 $EF$ 与平面 $BED$ 所成角的正弦值．标注答案直线 $EF$ 与平面 $BED$ 所成角的正弦值为 $\dfrac {\sqrt 5}{6}$解析先找到角，再通过解三角形求值．找角时，直接在 $ EF $ 上取点向面作垂线找角不利于后面的求值，可利用 $EF\parallel AB$，通过转化，在 $ AB $ 上取点向面作垂线找角求解．因为 $EF\parallel AB$，所以直线 $EF$ 与平面 $BED$ 所成角即为直线 $AB$ 与平面 $BED$ 所成角．
过点 $A$ 作 $AH\perp DE$ 于点 $H$，连接 $BH$．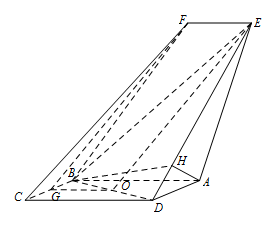
因为平面 $BED\cap 平面 AED=ED$，由 $(2)$ 知 $AH\perp 平面 BED$，所以直线 $AB$ 与平面 $BED$ 所成角即为 $\angle ABH$．
在 $\triangle ADE$ 中，$AD=1$，$DE=3$，$AE=\sqrt{6}$，由余弦定理可得 $\cos \angle ADE=\dfrac{2}{3}$．
所以 $\sin \angle ADE=\dfrac{\sqrt{5}}{3}$．
因此 $AH=AD\cdot \sin \angle ADE=\dfrac{\sqrt{5}}{3}$．
在 ${\mathrm {Rt}}\triangle AHB$ 中，$\sin \angle ABH=\dfrac{AH}{AB}=\dfrac{\sqrt{5}}{6}$，
所以直线 $EF $ 与平面 $BED$ 所成角的正弦值为 $\dfrac {\sqrt 5}{6}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
